|
"India is the world's most ancient civilization. Nowhere
on earth can you find such a rich and multi-layered tradition that has remained
unbroken and largely unchanged for at least five thousand years. Bowing low
before the onslaught of armies, and elements, India has survived every invasion,
every natural disaster, every mortal disease and epidemic, the double helix of
her genetic code transmitting its unmistakable imprint down five millennia to no
less than a billion modern bearers. Indians have demonstrated greater cultural
stamina than any other people on earth. The essential basis of Indian
culture is Religion in the widest and most general sense of the world. An
intuitive conviction that the Divine is immanent in everything permeated every
phase of life," says Stanley Wolpert.
Indic civilization has enriched every art and science
known to man. Thanks to India, we reckon from zero to ten with misnamed
"Arabic" numerals (Hindsaa - in Arabic means from India), and use a decimal system without which our modern
computer age would hardly have been possible.
Science and philosophy were
both highly developed disciplines in ancient India. However, because Indian
philosophic thought was considerably more mature and found particular favor
amongst intellectuals, the traditions persists that any early scientific
contribution came solely from the West, Greece in particular. Because of this erroneous belief, which is perpetuated by a wide variety of
scholars, it is necessary to briefly examine the history of Indian scientific
thought. Jawaharlal
Nehru wrote in his book The Discovery of
India: "Till recently
many European thinkers imagined that everything that was worthwhile had its
origins in
Greece
or
Rome
."
From the very earliest times, India had made its contribution to
the texture of Western thought and living. Michael Edwardes, author of British
India, writes that throughout the literatures of Europe, tales of Indian origin
can be discovered. European mathematics -
and, through them, the full range of European technical achievement – could
hardly have existed without Indian numerals. But until the beginning of European
colonization in Asia, India’s contribution was usually filtered through other
cultures.
"Many of the advances in the sciences that we
consider today to have been made in Europe were in fact made in India centuries
ago." - Grant Duff British Historian of India. Dr. Vincent Smith has
remarked, "India suffers today, in the estimation of the world, more
through the world's ignorance of the achievements of the heroes of Indian
history than through the absence or insignificance of such achievement."

Introduction
Beginning of Indian
Scientific Thought
Concept of Time
Physics
Mathematics
Grammar
Science
Education
Chemistry
and metallurgy
Shipbuilding and Navigation
Commerce
Wealth


Introduction
According to American Historian Will
Durant in his book,
The Story of
Civilizations - Our Oriental Heritage ISBN:
1567310125 1937 p.391-396:
 "From the time of
Megasthenes, who described
India to Greece ca 302 B.C., down to the eighteenth century, India was all a
marvel and a mystery to Europe. Marco Polo (1254-1323) pictured its western
fringe vaguely, Columbus blundered upon America in trying to reach it, Vasco da
Gama sailed around Africa to rediscover it, and merchants spoke rapaciously of
"the wealth of the Indies." "From the time of
Megasthenes, who described
India to Greece ca 302 B.C., down to the eighteenth century, India was all a
marvel and a mystery to Europe. Marco Polo (1254-1323) pictured its western
fringe vaguely, Columbus blundered upon America in trying to reach it, Vasco da
Gama sailed around Africa to rediscover it, and merchants spoke rapaciously of
"the wealth of the Indies."
" It is true that even across the Himalayan
barrier India has sent to us such questionable gifts as grammar and logic,
philosophy and fables, hypnotism and chess, and above all our numerals and our
decimal system. But these are not the essence of her spirit; they are trifles
compared to what we may learn from her in the future. As invention, industry,
and trade bind the continents more closely, and shall absorb, even in enmity,
some of its ways and thoughts."
"The indications are that
Mohenjadaro was at its height when Cheops built the first great pyramid; that it
had commercial, religious and artistic connections to Sumeria and Babylonia...as
Sir John Marshall
believes, Mohenjadaro
represents the oldest of all civilizations known."
Yaqubi (9th
century) Muslim historian has written:
"The
Hindus are superior to all other nations in intelligence and thoughtfulness.
They are more exact in astronomy and astrology than any other people.
"The
Siddhanta is a good proof of their intellectual powers; by this book the Greeks
and Persians have also profited. In medicine their opinion ranks first."
Al-Jahiz
9th century Muslim historian writes:
"The Hindus excel in
astrology, mathematics, medicine and in various other sciences. They have
developed to a perfection arts like sculpture, painting, and architecture. They
have collections of poetry, philosophy, literature and science of morals. From
India
we received the book called Kalilah wa Dimnah. These people have judgment and
are brave. They posses the virtues of cleanliness and purity. Contemplation has
originated with them."
(source: The
Vision of India - By Sisirkumar Mitra
p. 226).
The
medieval Arab scholar Sa'id Ibn Ahmad al-Andalusi (1029-1070)
wrote in his Tabaqat al-'umam, one of the
earliest books on history of sciences:
 "The
first nation to have cultivated science is India. ... India is known for the
wisdom of its people. Over many centuries, all the kings of the past have
recognized the ability of the Indians in all the branches of knowledge... The
kings of China have stated that the kings of the world are five in number and
all the people of the world are their subjects. They mentioned the king of
China, the king of India, the king of the Turks, the king of the Persians, and
the king of the Romans... They referred to the king of
India as the "king of wisdom" because of the Indians'
careful treatment of ulum (sciences) and all the branches of knowledge. ... The
Indians, known to all nations for many centuries, are the metal (essence) of
wisdom, the source of fairness and objectivity. They are people of sublime
pensiveness, universal apologues, and useful and rare inventions. ... To their
credit the Indians have made great strides in the study of numbers and of
geometry. They have acquired immense information and reached the zenith in their
knowledge of the movements of the stars (astronomy).... After all that they have
surpassed all other peoples in their knowledge of medical sciences.." "The
first nation to have cultivated science is India. ... India is known for the
wisdom of its people. Over many centuries, all the kings of the past have
recognized the ability of the Indians in all the branches of knowledge... The
kings of China have stated that the kings of the world are five in number and
all the people of the world are their subjects. They mentioned the king of
China, the king of India, the king of the Turks, the king of the Persians, and
the king of the Romans... They referred to the king of
India as the "king of wisdom" because of the Indians'
careful treatment of ulum (sciences) and all the branches of knowledge. ... The
Indians, known to all nations for many centuries, are the metal (essence) of
wisdom, the source of fairness and objectivity. They are people of sublime
pensiveness, universal apologues, and useful and rare inventions. ... To their
credit the Indians have made great strides in the study of numbers and of
geometry. They have acquired immense information and reached the zenith in their
knowledge of the movements of the stars (astronomy).... After all that they have
surpassed all other peoples in their knowledge of medical sciences.."
“That which has reached us from the discoveries of their clear
thinking and the marvels of their inventions is the (game) of chess. The Indians
have, in the construction of its cells, its double numbers, its symbols and
secrets, reached the forefront of knowledge. They have extracted its mysteries
from supernatural forces. While the game is being played and its pieces are
being maneuvered, there appear the beauty of structure and the greatness of
harmony. It demonstrates the manifestation of high intentions and noble deeds,
as it provides various forms of warnings from enemies and points out ruses as
well as ways to avoid dangers. And in this, there is considerable gain and
useful profit.”
(source: The
Categories of Nations
- By
Said al-Andalusi.
A translation was published by
University
of
Texas Press
: “Science in the Medieval World”. This is the first English translation of
this eleventh-century manuscript. Quotes are from Chapter V: “Science in
India
”). A
Concise History of Science in
India
eds.
D. M. Bose, S. N. Sen & B. V. Subbarayappa.
New Delhi
.
Indian
National
Science
Academy
, 1989), p. i and The
Invasion That Never Was - By Michel Danino and Sujata Nahar
p. 16 and How
'Gandhara' became 'Kandahar' - By Rajiv Malhotra and The
Making of the Indo-Islamic World. Volume I – Early Medieval India and the
Expansion of Islam 7th-11th Centuries - By Andre Wink.
Oxford
University
Press,
New Delhi
1999. p.112 -193).
Abu’l Hasan al-Qifti ( ? ) Arab
scholar and author of Chronology of the Scholars, speaks of Arab admiration for Indian place-value system and
methods of calculation.
“Among those parts of their sciences which came to us, the
numerical calculation….it is the swiftest and most complete method of
calculation, the easiest to understand and the simplest to learn; it bears
witness to the Indians’ piercing intellect, fine creativity and their superior
understanding and inventive genius.”
(source: The
Universal History of Numbers - By Georges Ifrah p. 530 -
531).
For
more refer to chapter on Quotes.
Sir William Wilson Hunter
( ? )author of the book, The
Indian Empire, said India," has even contributed to modern
medical science by the discovery of various chemicals and by teaching you how to reform
misshapen ears and noses. Even more it has done in mathematics, for algebra, geometry,
astronomy, and the triumph of modern science -- mixed mathematics -- were all invented in
India, just so much as the ten numerals, the very cornerstone of all present
civilization,
were discovered in India, and are in reality, Sanskrit words."
 Beginning with the earliest known Indian civilization,
the Indus Valley, with its pottery wheel, cotton textiles, Indus script, and two
wheeled carts, there is a good deal of material and texts to work from. By the
beginning of the third millennium B.C. in India, as in China, Egypt, and
Mesopotamia, scientific development was well advanced. Excavations
carried on at the sites of the Indus civilization have revealed remnants of an
ancient civilization unsurpassed in civil engineering accomplishments,
particularly baths and drainage. Whilst much is
known of the hygienic measures of the period, little is known of the scientific
knowledge upon which it was based. From the town Planning and Great Baths of Indus Valley
it is evidence in the neat arrangement of the major buildings contained in the citadel, including
the placement of a large granary and water tank or bath at right angles to one another.
The lower city, which was tightly packed with residential units, was also constructed on a
grid pattern consisting of a number of blocks separated by major cross streets.
Baked-brick houses faced the street, and domestic life was centered around an enclosed
courtyard.
The cities had an elaborate public drainage system, Sanitation was provided through an
extensive system of covered drains running the length of the main streets and connected by
chutes with most residences. In
the valley of the Indus River of India, the world's oldest civilization had
developed its own system of mathematics. Beginning with the earliest known Indian civilization,
the Indus Valley, with its pottery wheel, cotton textiles, Indus script, and two
wheeled carts, there is a good deal of material and texts to work from. By the
beginning of the third millennium B.C. in India, as in China, Egypt, and
Mesopotamia, scientific development was well advanced. Excavations
carried on at the sites of the Indus civilization have revealed remnants of an
ancient civilization unsurpassed in civil engineering accomplishments,
particularly baths and drainage. Whilst much is
known of the hygienic measures of the period, little is known of the scientific
knowledge upon which it was based. From the town Planning and Great Baths of Indus Valley
it is evidence in the neat arrangement of the major buildings contained in the citadel, including
the placement of a large granary and water tank or bath at right angles to one another.
The lower city, which was tightly packed with residential units, was also constructed on a
grid pattern consisting of a number of blocks separated by major cross streets.
Baked-brick houses faced the street, and domestic life was centered around an enclosed
courtyard.
The cities had an elaborate public drainage system, Sanitation was provided through an
extensive system of covered drains running the length of the main streets and connected by
chutes with most residences. In
the valley of the Indus River of India, the world's oldest civilization had
developed its own system of mathematics.
This civilization is known for its
well planned cities, brick built houses, excellent drainage system
and water storage tanks. Benjamin Rowland
(1904-1972) author of Art
and Architecture of India wrote: "Indeed it
could be said that the population of the Indus cities lived more
comfortably than did their contemporaries in the crowded and
ill-built metropolises elsewhere. People were literate and had their
own script. Dance and music formed essential part of their daily
life."
 They
had wide main streets and were magnificently laid out in grid form, reflecting
careful town planning. They had sewers, municipal water systems, public baths,
and well-fortified citadels. The private houses were well built, of fine solid
baked bricks which have not crumbled over the centuries. Many of them were two
stories high, and had seat latrines and chutes for refuse. Homes were built
around courtyards. The people of the Indus Valley civilization had an advanced
technology. They knew how to make cotton cloth and copper and bronze castings
and forgings. Some of
their art objects have a wonderful simple realism. The torso of one small
dancing figure is so unbelievably alive that one can almost feel the easy
muscles at work under the smooth skin. They
had wide main streets and were magnificently laid out in grid form, reflecting
careful town planning. They had sewers, municipal water systems, public baths,
and well-fortified citadels. The private houses were well built, of fine solid
baked bricks which have not crumbled over the centuries. Many of them were two
stories high, and had seat latrines and chutes for refuse. Homes were built
around courtyards. The people of the Indus Valley civilization had an advanced
technology. They knew how to make cotton cloth and copper and bronze castings
and forgings. Some of
their art objects have a wonderful simple realism. The torso of one small
dancing figure is so unbelievably alive that one can almost feel the easy
muscles at work under the smooth skin.
(source:
India:
A World in Transition - By Beatrice Pitney Lamb
p. 20).
"Mohenjo-daro had some of the most advanced toilets and
sewers, with lavatories built into the outer walls of houses. There were
“Western-style” toilets made from bricks with wooden seats on top. They had
vertical chutes, through which waste fell into street drains or cesspits. Sir
Mortimer Wheeler, the director-general of archaeology in India from 1944 to
1948,
wrote: “The high quality of the sanitary arrangements
could well be envied in many parts of the world today.”
Nearly all of the hundreds of houses excavated had their own
bathing rooms. Generally located on the ground floor, the bath was made of
brick, sometimes with a surrounding curb to sit on. The water drained away
through a hole in the floor, down chutes or pottery pipes in the walls, into the
municipal drainage system. Even the fastidious
Egyptians rarely had special bathrooms."
The Indian architects designed sewage disposal systems on a
large scale, building networks of brick effluent drains following the lines of
the streets. The drains were seven to ten feet wide, cut at two feet below
ground level with U shaped bottoms lined with loose brick easily taken up for
cleaning. At the intersection of two drains, the sewage planners installed
cesspools with steps leading down into them, for periodic cleaning. By 2700 B.C.
these cities had standardized earthenware plumbing pipes with broad flanges for
easy joining with asphalt to stop leaks."
The Harappans employed a
variety of plumb bobs that reveal a system of weight based on a decimal scale.
For example, a basic Harappan plumb bob weighs 27.584 grams. If we assign that a
value of 1, other weights scale in at 0.5, .1., 2, .5, 2, 5, 10, 20 50, 100,
200, and 500. Archaeologists have found a “ruler” made of shell lines drawn
6.7 millimeters apart with a high degree of accuracy. Two of the lines are
distinguished by circles and are separated by 33.5 millimeters or 1.32 inches.
This distance is the so-called Indus inch.
Harappan
bricks contain no straw or binding material and are still in usable shape after
five thousand years. Most interesting are their dimensions: while
found in fifteen different sizes, their length, width, and thickness are always
in the ration of 4:2:1.
(source:
Lost
Discoveries - Dick Teresi
p. 351-352 and 59 - 62).
 In ancient India, as in Greece, there was much
speculative thought about astronomy, mathematics, physics, and biology. But
mathematics and mysticism were inextricably mixed in early Greek thought, and
Greek belief in magic, divination and oracles was perhaps more pronounced than
its counterpart in India. In ancient India, as in Greece, there was much
speculative thought about astronomy, mathematics, physics, and biology. But
mathematics and mysticism were inextricably mixed in early Greek thought, and
Greek belief in magic, divination and oracles was perhaps more pronounced than
its counterpart in India.
It is therefore untrue to assert, as recent European
writers particularly have done, that Greece was the home of pure science.
Both
India and Greece, whilst having their own traditions, had direct and indirect
effects on each other in science as they did in philosophy. In fact, long before
the Greeks, the Indians had learned to employ the dialectic method to grasp
empirical and transcendental truths, although in India, more perhaps than in
ancient Greece or the modern West, reason and truth, logic and mysticism, the
visible and invisible, have always been regarded as inseparable. The practical
application of science to human affairs, was as poor in India as it was in any
other ancient society. In fact, this was not achieved until the eighteenth
century, until then science and technology developed separately. When
it did as in the case of Galileo Galilei, who was the first to employ the modern
scientific method in its fullness, he incurred the wrath of the Church and was
incarcerated by the Inquisition at the advanced age of seventy. There is hardly
any parallel in India where a difference in interpretation either in metaphysics
or scientific thought was so unkindly suppressed.
 The spirit of scientific enquiry and a rigorous
correlation of cause and effect in explaining natural phenomenon were
particularly evident in ancient India. The connection between Indian philosophy
and medicine, mathematics, astronomy, and technology is, strangely enough seldom
realized much less recognized. The spirit of scientific enquiry and a rigorous
correlation of cause and effect in explaining natural phenomenon were
particularly evident in ancient India. The connection between Indian philosophy
and medicine, mathematics, astronomy, and technology is, strangely enough seldom
realized much less recognized.
Ancient Indians "measured the land, divided the
year, mapped out the heavens, traced the course of the sun and the planets
through the zodiacal belt, analyzed the constitution of matter, and studied the
nature of birds and beasts, plants and seeds." Whilst in Western civilizations the interest has been increasingly focused
on single sciences, in the Indian world the ontological viewpoint has been
generally preferred, and it would appear that "in India, through all
periods, the special sciences are rooted in and developed on the
underlying cosmic concepts and presuppositions. This universal vision in India
has never been lost.
India's contribution to the
sciences of mathematics and medicine have been unique. In other sciences,
especially linguistics, metallurgy, and chemistry, Indians made trail-blazing
discoveries.
(source: An
Introduction to India - By Stanley Wolpert p. 192).
The Vedic Shulba Sutras
(fifth to eighth century B.C. E.) meaning "codes
of the rope,"
show that the earliest geometrical and mathematical
investigations among the Indians arose from certain requirements of their
religious rituals. When the poetic vision of the Vedic seers was externalized in
symbols, rituals requiring altars and precise measurement became manifest,
providing a means to the attainment of the unmanifest world of consciousness.
"Shulba Sutras" is the name given to those portions or supplements of
the Kalpasutras, which deal with the measurement and construction of the
different altars or arenas for religious rites. The word Shulba refers to the
ropes used to make these measurements.
Although Vedic mathematicians are known primarily for their computational genius
in arithmetic and algebra, the basis and inspiration for the whole of Indian
mathematics is geometry. Evidence of geometrical drawing instruments from as
early as 2500 B.C.E. has been found in the Indus Valley.
 The
beginnings of algebra can be traced to the constructional geometry of the Vedic
priests, which are preserved in the Shulba Sutras. Exact measurements,
orientations, and different geometrical shapes for the altars and arenas used
for the religious functions (yajnas), which occupy an important part of the
Vedic religious culture, are described in the Shulba Sutras. Many of these
calculations employ the geometrical formula known as the Pythagorean theorem. The
beginnings of algebra can be traced to the constructional geometry of the Vedic
priests, which are preserved in the Shulba Sutras. Exact measurements,
orientations, and different geometrical shapes for the altars and arenas used
for the religious functions (yajnas), which occupy an important part of the
Vedic religious culture, are described in the Shulba Sutras. Many of these
calculations employ the geometrical formula known as the Pythagorean theorem.
This theorem (c. 540
B.C.E.),
equating the square of the hypotenuse of a right angle triangle with the sum of
the squares of the other two sides, was utilized in the earliest Shulba Sutra
(the Baudhayana) prior to the eighth century B.C.E. Thus, widespread use of this
famous mathematical theorem in India several centuries before its being
popularized by Pythagoras has been documented. The exact wording of the theorem
as presented in the Sulba Sutras is: "The diagonal chord of the rectangle
makes both the squares that the horizontal and vertical sides make
separately." The
proof of this fundamentally important theorem is well known from Euclid's time
until the present for its excessively tedious and cumbersome nature; yet the
Vedas present five different extremely simple proofs for this theorem.
One
historian, Joseph
Needham,
has stated, "Future research on the history of science and technology in
Asia will in fact reveal that the achievements of these peoples contribute far
more in all pre-Renaissance periods to the development of world science than has
yet been realized."
Meticulous
planning and architectural brilliance in the layout of the city are
the established and striking features of the Harappan civilisation.
Recent excavations at the
small township of Dholavira, in Kutch, Gujarat, have presented to
the world some of the oldest stadiums and
sign board.
One of the stadiums is huge. The
multipurpose structure, with terraced seats for spectators, around
800 feet in length (around 283 metres) can accommodate as many as
10,000 persons. The other stadium is
much smaller in size.
The dimensions of the town of
Dholavira (777.1 metres in length and 668.7 meters in width)
establishes that the Harappans had great knowledge of
trigonometry. They were also mathematical experts as all the
dimensions at the site are based on squares and cubes,
(source: Oldest
Harappan signboard at Kutch township - timesofindia.com).
Refer to
Marco Polo’s epic journey to China was a big con –
Team Folks
Ancient
Indians already operated with a time span of astronomical proportions long
before the earliest signs of natural science in ancient Greece. It
is undeniable that ancient Indian texts present astonishingly exact scientific
calculations even by today's latest scientific standards, such as the speed of
light, exact size of the smallest particles and the age of the universe.
The
Surya Siddhanta, a textbook on astronomy of
ancient India - last compiled in 1000 BC, believed by Hindus to be handed down
from 3000 BC by aid of complex mnemonic recital methods still known today - computed
the earth's diameter to be 7,840 miles, the distance earth - moon as 253,000
miles. These compare to modern measurements resp. as 7,926.7 miles and 252,710
miles for max. dist. moon-earth.
Manu's
texts in Sanskrit propounded evolution thousands of years before Lamarck &
Darwin. "The first germ of life was developed by water and heat. Man will
traverse the universe, gradually ascending and passing through the rocks, the
plants, the worms, insects, fish, serpents, tortoises, wild animals, cattle, and
higher animals. These are the transformations declared, from the plant to
Brahma, which have to take place in the world."
Brihath
Sathaka operates with divisions of the time
of one day into:- 60 kalas or ghatika - 24 mins each. Subdivided into 60 vikala
(24 secs.each) 60 para then into tatpara, then into vitatpara then into ima then
into kasha.... the smallest unit, equal to approx. o.ooooooo3 of a second (one
300 millionth). This smallest unit (3 X 10 -8 second) is surprisingly close to
the life-spans of certain mesons and hyperons, according to some Western
physicist who was interviewed on the BBC World Service in the early 1990s.
The 14th century 'Rigveda
of the Sun' (dated by manuscript age only), says that the sun covers 2,202
yoganas in half a mimesa - which calculates as 300,000 metres a second, fairly
exactly the speed of light.
(source: Science,
the Critical mind and Dissent - By Robert C Priddy).
Watch
Carl
Sagan and Hindu cosmology – video
 Francois
Marie Arouet Voltaire (1694-1774)
France's greatest writers and philosophers, was a theist, and a bitter critic
of the Church said : Francois
Marie Arouet Voltaire (1694-1774)
France's greatest writers and philosophers, was a theist, and a bitter critic
of the Church said :
"
It is very important to note that some 2,500 years ago at the least Pythagoras
went from Samos to the Ganges to learn geometry...But he would certainly not
have undertaken such a strange journey had the reputation of the Brahmans'
science not been been long established in Europe....We have already acknowledged
that arithmetic, geometry, astronomy were taught among the Brahmans. From time
immemorial they have known the precession of the equinoxes and were in their
calculation far closer to the real figure than the Greeks who came much later.
Mr. Le Gentil (a French astronomer who spent several years in India) has with
admiration acknowledged the Brahmans' science, as well as the immensity of time
these Indians must have needed to reach a knowledge of which even the Chinese
never had any notion, and which was unknown to Egypt and to Chaldea, the teacher
of Egypt."
(source:
Fragments historiques sur l'linde - By Voltaire
p. 444 - 445.). For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Top
of Page
Beginning of Indian Scientific Thought
 The beginning of Indian scientific thought are traced
to the same source as those of Indian metaphysics and religion, the Rig
Veda. The Vedas, being essentially works of poetic imagination, cannot be
expected to contain much spirit of scientific inquiry, yet there are remarkable
flashes of intuitive conjecture and reason. The beginning of Indian scientific thought are traced
to the same source as those of Indian metaphysics and religion, the Rig
Veda. The Vedas, being essentially works of poetic imagination, cannot be
expected to contain much spirit of scientific inquiry, yet there are remarkable
flashes of intuitive conjecture and reason.
They explain the nature of the universe,
of life, while admitting that Creation itself is the one unknowable mystery.
To
the Vedic sages, creation indicated that point before which there was no
Creator, the line between indefinable nothingness and something delineated by
attributes and function, at least. Like the moment before the Big Bang Theory.
These concepts preoccupy high wisdom, the Truth far removed from mere religion.
Indeed,
in one of the most remarkable of the Vedic hymns -
In
the Hymn of Creation (Rig Veda 10.129.3)
a searching inquiry as to the origin of the world is made; it is certainly the
earliest known record of philosophic doubt.

"
There was not non-existent nor existent;
There was no realm of air, no sky beyond it.
What covered it, and where? and what gave shelter?
Was water there, unfathomed depth
of water?
Yet the Vedas go further, being
philosophy, or really spiritual sciences, rather than myth.
The
hymn goes to say that in the beginning there was neither death nor immortality,
nor day nor night. All that existed was void and formless. Then arose, desire,
the primal seed and germ of spirit. But,
Who verily knows and
who can declare it,
Whence it was born and
Whence comes this creation?
The gods are later than this
world's production
Who knows, then, whence it
first came into being?
 Vedas
are the most sophisticated, most profoundly
beautiful, and most complete presentations of what Aldous Huxley termed the
“perennial philosophy” that is at the core of all religions. In modern
academia, of course, there is not supposed to be any “ancient wisdom”. In this hymn, which
contains the essence of monism, can be seen a representation of the most
advanced theory of creation. The germ of free speculation and skepticism were
already present in the Rig Veda. Vedas
are the most sophisticated, most profoundly
beautiful, and most complete presentations of what Aldous Huxley termed the
“perennial philosophy” that is at the core of all religions. In modern
academia, of course, there is not supposed to be any “ancient wisdom”. In this hymn, which
contains the essence of monism, can be seen a representation of the most
advanced theory of creation. The germ of free speculation and skepticism were
already present in the Rig Veda.
(source: The Empire of the Soul:
Some Journeys into India - By Paul William Roberts published
by Riverhead Books ASIN: 1573226351 p
300-301).
The statue of Nataraja (dance pose of
Lord Shiva) is a well known example for the artistic, scientific and
philosophical significance of Hinduism.
Freedom
was born in India. Doubt, the
mother of freedom, was born with the Rig Veda,
the most sacred scripture of the Hindus which has the following:
What are words, and what are mortal thoughts!
Who is there who truly knows and who can say,|
Whence this unfathomed world
And from what cause!
Freedom
of the mind created the wondrous world of the intellect — the world of Hindu
rishis, philosophers, poets and dramatists. It was the freedom of the mind and
freedom of the senses which led to India’s diversity and contributed to the
richness of its civilization. No other civilization, not even that of the
Greeks, could have enjoyed the freedom that we had. We have to remember,
Socrates was forced to drink hemlock! The Inquisition burnt the Christian
apostates at the stake and Islam beheaded dissenters.
Watch
Carl
Sagan and Hindu cosmology – video
Top
of Page
Concept of Time
"After a cycle of universal
dissolution, the Supreme Being decides to recreate the cosmos so that we souls
can experience worlds of shape and solidity. Very subtle atoms begin to combine,
eventually generating a cosmic wind that blows heavier and heavier atoms
together. Souls depending on their karma earned in previous world systems,
spontaneously draw to themselves atoms that coalesce into an appropriate
body." - The
Prashasta Pada.
***
Grandiose time scales
Hinduism’s
understanding of time is as grandiose as time itself. While most cultures base
their cosmologies on familiar units such as few hundreds or thousands of years,
the Hindu concept of time embraces billions and trillions of years. The
Puranas describe time units from the infinitesimal
truti, lasting 1/1,000,0000 of a second to a mahamantavara of 311 trillion
years. Hindu sages describe time as cyclic, an endless procession of
creation, preservation and dissolution. Scientists such as Carl Sagan have
expressed amazement at the accuracy of space and time descriptions given by the
ancient rishis and saints, who fathomed the secrets of the universe through
their mystically awakened senses.
(source: Hinduism Today April/May/June 2007
p. 14).
As in modern physics, Hindu
cosmology envisaged the universe as having a cyclical nature. The end of each
kalpa brought about by Shiva's dance is also the beginning of the next. Rebirth
follows destruction.
 The transcendence of time is
the aim of every Indian spiritual tradition. Time is often presented as an eternal wheel
that binds the soul to a mortal existence of ignorance and suffering. "Release"
from time's fateful wheel is termed
moksha, and an advanced ascetic may be called
kala-attita
(' he who has transcended time'). The transcendence of time is
the aim of every Indian spiritual tradition. Time is often presented as an eternal wheel
that binds the soul to a mortal existence of ignorance and suffering. "Release"
from time's fateful wheel is termed
moksha, and an advanced ascetic may be called
kala-attita
(' he who has transcended time').
Hindus believe that the universe is without a beginning (anadi= beginning-less) or an
end (ananta =
end-less). Rather the universe is projected in cycles.
Time immemorial is measured in cycles called Kalpas. A Kalpa
is a day and night for Brahma, the Lord of Creation. After each Kalpa, there is
another Kalpa. Each Kalpa is composed of 1,000 Maha Yugas.
A Kalpa is thus equal to 4.32 billion human years. Kirtha
Yuga or Satya yuga (golden or truth age) is 1,728,000 years; Treta yuga is
1,296,000 years; Dvapara yuga is 864,000 years; and Kali Yuga is 432,000
years. Total duration of the four yugas is called a kalpa. At the end of kalyuga the universe is dissolved by pralaya (cosmic
deluge ) and another cycle begins. Each cycle of creation lasts one kalpa, that is
12,000,000 human years ( or 12,000 Brahma years).
One Maha Yuga is 4,32 million years.
| Krita or Satya |
golden age |
1,728,000
years |
| Treta |
silver age |
1,296,000
years |
| Dvapara |
copper age |
864,000
years |
| Kali |
iron age |
432,000
years |
Watch
Carl
Sagan and Hindu cosmology – video
A Brahma, or Lord of Creation, lives for one hundred Brahma
years (each of made up of 360 Brahma days). After that he dies. So a Brahma
lives for 36,000 Kalpas, or 36,000 x 2,000 x 4,30,000 human years – i.e., a
Brahma lives for 311.4 trillion human years. After the death of each Brahma,
there is a Mahapralaya or Cosmic deluge,
when all the universe is destroyed. Then a new Brahma appears and creation
starts all over again.
(source: Am
I a Hindu - by Ed Viswanathan p. 292 - 293). For more on
Yugas, refer to
One
Cosmic Day of Creator Brahma).
Refer to
Sciences of the Ancient Hindus: Unlocking Nature in
the Pursuit of Salvation – By Alok Kumar
Time in Hindu mythology is conceived as a wheel turning through
vast cycles of creation and destruction (pralaya), known as kalpa. In the words of
famous writer, Joseph
Campbell:
"The Hindus with their grandiose Kalpas and their ideas of the
divine power which is beyond all human category (male or female). Not so alien to the
imagery of modern science that it could not have been put to acceptable use."
According to
Guy Sorman,
visiting scholar at Hoover Institution at Stanford and the leader of new
liberalism in France:
"Temporal notions in
Europe were overturned by an India rooted in eternity. The
Bible had been the yardstick for measuring time, but the infinitely vast time
cycles of India suggested that the world was much older than anything the Bible
spoke of. It seem as if the Indian mind was better
prepared for the chronological mutations of Darwinian evolution and
astrophysics."
(source: The
Genius of India - By Guy Sorman ('Le Genie de l'Inde')
Macmillan India Ltd. 2001. ISBN 0333 93600 0 p.
195). For more on Guy Sorman refer to chapter Quotes201_220).(Refer
to Visions
of the End of the World - By Dr. Subhash Kak - sulekha.com).
 Huston Smith
a philosopher, most
eloquent writer, world-famous religion scholar who practices
Hatha Yoga. Has taught at MIT and is currently
visiting professor at Univ. of California at Berkley. Smith has
also produced PBS series. He has written various books, The
World's Religions, "Science and Human
Responsibility", and "The Religions of Man" says: Huston Smith
a philosopher, most
eloquent writer, world-famous religion scholar who practices
Hatha Yoga. Has taught at MIT and is currently
visiting professor at Univ. of California at Berkley. Smith has
also produced PBS series. He has written various books, The
World's Religions, "Science and Human
Responsibility", and "The Religions of Man" says:
“Philosophers tell us that the Indians were the first ones
to conceive of a true infinite from which nothing is excluded.
The West shied away from this notion. The West likes form,
boundaries that distinguish and demarcate. The trouble is that
boundaries also imprison – they restrict and confine.”
“India saw this clearly and turned
her face to that which has no boundary or whatever.” “India
anchored her soul in the infinite seeing the things of the world
as masks of the infinite assumes – there can be no end to
these masks, of course. If they express a true infinity.” And
It is here that India’s mind boggling variety links up to her
infinite soul.”
“India includes so much because her soul being infinite
excludes nothing.” It goes without saying that the universe
that India saw emerging from the infinite was stupendous.”
While the West was still thinking,
perhaps, of 6,000 years old universe – India was already
envisioning ages and eons and galaxies as numerous as the sands
of the Ganges. The Universe so vast that modern astronomy slips
into its folds without a ripple.”
(source: The
Mystic's Journey - India
and the Infinite: The Soul of a People – By Huston Smith).
For more on Huston Smith refer to chapter Quotes41_60).
 Dr.
Carl Sagan in his book Broca's
Brain: Reflections on the Romance of Science,
remarks: Dr.
Carl Sagan in his book Broca's
Brain: Reflections on the Romance of Science,
remarks:
"Immanuel
Velikovsky
(the author of Earth in Upheaval)
in his book Worlds
in Collision, notes that the idea of four ancient ages terminated
by catastrophe is common to Indian as well as to Western sacred writing.
However,
in the Bhagavad
Gita and in the Vedas,
widely divergent numbers of such ages, including an infinity of them, are given;
but, more interesting, the duration of the ages between major catastrophes is
specified as billions of years. .. "
"The
idea that scientists or theologians, with our present still puny understanding
of this vast and awesome cosmos, can comprehend the origins of the universe is
only a little less silly than the idea that Mesopotamian astronomers of 3,000
years ago – from whom the ancient Hebrews borrowed, during the Babylonian
captivity, the cosmological accounts in the first chapter of Genesis – could
have understood the origins of the universe. We simply do not know.
The
Hindu holy book, the Rig
Veda (X:129), has a much more realistic
view of the matter:
“Who
knows for certain? Who shall here declare it?
Whence was it born, whence came creation?
The gods are later than this world’s formation;
Who then can know the origins of the world?
None knows whence creation arose;
And whether he has or has not made it;
He who surveys it from the lofty skies,
Only he knows- or perhaps he knows not."
(source:
Broca's
Brain: Reflections on the Romance of Science - By Carl Sagan
p. 106 - 137). Watch
Carl
Sagan and Hindu cosmology – video
The theory of animal life and particularly of man
was correctly understood by the ancient thinkers. The Brihat
Vishnu Purana states that "the aquatic life precedes the monkey
life" and that "the monkey life is the precursor of the human
life." The same theory was explained in an interesting way by the
dashavatara (ten incarnations). But evolution, as everything else, was the
manifestation of the supreme spirit (Atman) as is testified by Chandogya
Upanishad.
(source: Ancient Indian History and Culture - By Chidambara
Kulkarni Orient Longman Ltd. 1974. p.268).
 Hinduism is the only religion that propounds the idea
of life-cycles of the universe. It suggests that the universe undergoes an
infinite number of deaths and rebirths. Hinduism, according to Carl
Sagan, "... is the only religion in which the time scales
correspond... to those of modern scientific cosmology. Its cycles run from our
ordinary day and night to a day and night of the Brahma, 8.64 billion years
long, longer than the age of the Earth or the Sun and about half the time since
the Big Bang" Hinduism is the only religion that propounds the idea
of life-cycles of the universe. It suggests that the universe undergoes an
infinite number of deaths and rebirths. Hinduism, according to Carl
Sagan, "... is the only religion in which the time scales
correspond... to those of modern scientific cosmology. Its cycles run from our
ordinary day and night to a day and night of the Brahma, 8.64 billion years
long, longer than the age of the Earth or the Sun and about half the time since
the Big Bang"
Long before Aryabhata
(6th century) came up with this awesome achievement, apparently there was a
mythological angle to this as well -- it becomes clear when one looks at the
following translation of Bhagavad Gita (part
VIII, lines 16 and 17),
"All the planets
of the universe, from the most evolved to the most base, are places of
suffering, where birth and death takes place. But for the soul that reaches my
Kingdom, O son of Kunti, there is no more reincarnation. One day of Brahma is
worth a thousand of the ages [yuga] known to humankind; as is each
night."
Thus each kalpa is worth one day in the life of
Brahma, the God of creation. In other words, the four ages of the mahayuga
must be repeated a thousand times to make a "day ot Brahma", a unit of
time that is the equivalent of 4.32 billion human years, doubling which one gets
8.64 billion years for a Brahma day and night. This was later theorized
(possibly independently) by Aryabhata in the 6th century. The cyclic nature of
this analysis suggests a universe that is expanding to be followed by
contraction... a cosmos without end. This, according to modern physicists is not
an impossibility.
(source: Astronomy
and Mathematics in Ancient India).
 Count Maurice
Maeterlinck (1862-1949) was a Belgian writer of poetry, a wide
variety of essays. He won the 1911 Nobel Prize for literature. In his book Mountain
Paths, says: Count Maurice
Maeterlinck (1862-1949) was a Belgian writer of poetry, a wide
variety of essays. He won the 1911 Nobel Prize for literature. In his book Mountain
Paths, says:
"he falls back upon
the earliest and greatest of Revelations, those of the Sacred Books of India
with a Cosmogony which no European conception has ever surpassed."
(source: Mountain
Paths - By Maurice Maeterlinck).
In Hindu thought,
interspersed between linear, time-limited existences lie timeless intervals of
non-existence. The creation hymn of the Hindus, Nasadiya-sukta of Rig-Veda,
affirms an absolute beginning of things and describes the origin of the universe
as being beyond the concepts of existence and non-existence
“The Hindu ... pictured the universe as periodically
expanding and contracting and gave the name Kalpa to the time span between the
beginning and the end of one creation. The scale of this space or time is indeed
staggering. It has taken more than two thousand years to come up again with a
similar concept.”
Hindu culture had this unique vision of the
infiniteness of time as well as the infinity of space. When modern astronomy
deals with billion of years, Hindu creation concepts deal with trillions of
years. Vedanta upholds the idea that
creation is timeless, having no beginning in time. Each creation and dissolution
follows in sequence. The whole cosmos exists in two states -- the unmanifested
or undifferentiated state and the manifested or differentiated state.
(source: The
Origin of the Universe - By K B N Sarma - sulekha.com).
John Bowle,
categorically declares that Plato was influenced by
Indian ideas.
(source: A
New Outline of World History - By John Bowle p. 91).
 Princeton
University’s Paul Steinhardt and Cambridge
University’s Neil Turok, have recently
developed The Cyclical Model. Princeton
University’s Paul Steinhardt and Cambridge
University’s Neil Turok, have recently
developed The Cyclical Model.
They
have just fired their latest volley at
that belief, saying there could be a timeless cycle of
expansion and contraction. It’s an idea as old as Hinduism, updated for the
21st century. The
theorists acknowledge that their cyclic concept draws upon religious and
scientific ideas going back for millennia — echoing the "oscillating
universe" model that was in vogue in the 1930s, as well as the Hindu belief
that the universe has no beginning or end, but follows a cosmic cycle of
creation and dissolution.
(source: Questioning
the Big Bang
- msnbcnews.com).
 Dr.
Alok Kumar professor of Physics at the State University of New York
at Oswego and author of the new book, Sciences of the
Ancient Hindus has observed: Dr.
Alok Kumar professor of Physics at the State University of New York
at Oswego and author of the new book, Sciences of the
Ancient Hindus has observed:
"What would
you say about the people or culture who gave us the place-value system of
numerals, the numerical zero, the trigonometric function “sine” and several
trigonometric formulae, and set standards for mass, length, and time? What about
those who developed a sophisticated system of medicine with its mind-body
approach known as Ayurveda, detailed anatomical and surgical knowledge of the
human body, metallurgical methods of extraction and purification of metals
including the so called Damascus blade, chemical techniques to transform
compounds, knowledge of various constellations and planetary motions that was
good enough to assign motion to the Earth in the fifth century A.D. and the
science of self-improvement (Yoga)?
The ancient Hindus used a complex
calendar that used the sun and the moon in defining the day, month and year.
While days and months were defined by the moon, the year was defined by the sun.
Regarding the Earth’s motion, Aryabhatta I suggested about one millennium before
Copernicus a theory in which the Earth was in axial rotation. All stars, but not
planets, were at rest in this theory. Aryabhata I’s hypothesis of the Earth’s
rotational motion is clearly explained by the analogy of a boatman who observes
objects on the shore moving backward.
Science was institutionalized
among the ancient Hindus. It was considered sacred and as good as their moral
codes for society. Scientific activities had important functions that were
valued in society. The role of astronomers to fix the calendar, to set dates of
religious festivals, and to predict eclipses or other astronomical events became
as important as their moral codes.
"There is no scholarly tradition
in India to visit foreign lands for learning. On the contrary, India attracted
scholars from China, the Middle East, and even from the Mediterreanean. This is
in contrast to the Greek tradition in which many young Greek scholars undertook
arduous
journeys to Egypt, Babylon,
Persia, and even to India for learning. "
(source:
Sciences of the Ancient Hindus - by Alok Kumar p. 12 - 13 and p. 24 -31).
 Dick Teresi
( ? ) author and coauthor of several books about
science and technology, including The
God Particle. He is cofounder of Omni
magazine and has written: Dick Teresi
( ? ) author and coauthor of several books about
science and technology, including The
God Particle. He is cofounder of Omni
magazine and has written:
"The big
bang is the biggest-budget universe ever, with mind-boggling
numbers to dazzle us – a technique pioneered by fifth-century
A.D. Indian cosmologists, the first to
estimate the age of the earth at more than 4 billion years. The cycle of
creation and destruction continues forever, manifested in the Hindu
deity Shiva, Lord of the Dance, who holds the drum
that sounds the universe’s creation in his right hand and the
flame that, billions of years later, will destroy the universe
in his left. Meanwhile Brahma is but one of untold numbers of
other gods dreaming their own universes.
The 8.64
billion years that mark a full day-and-night cycle in Brahma’s
life is about half the modern estimate for the age of the
universe. The ancient Hindus believed that each Brahma day and
each Brahma night lasted a kalpa, 4.32 billion years, with
72,000 kalpas equaling a Brahma century, 311,040 billion years
in all. That the Hindus could conceive of the universe in terms
of billions."
(source: Lost
Discoveries: The Ancient Roots of Modern Science - By Dick
Teresi p.
159 and 174 -212).
The Hindus, according to Sir
Monier-Williams, were Spinozists more than
2,000 years before the advent of Spinoza, and Darwinians many centuries before Darwin and
Evolutionists many centuries before the doctrine of Evolution was accepted by scientists
of the present age.
The French historian
Louis Jacolliot
says, "Here to mock are conceit, our apprehensions, and our
despair, we may read what Manu
said, perhaps 10,000 years before the birth of Christ about Evolution:
' The first germ of life was
developed by water and heat.' (Book I, sloka 8,9 )
' Water ascends towards the sky in vapors; from the sun it descends in rain, from the rains
are born the plants, and from the plants, animals.' (Book III, sloka 76).
(source:
Philosophy of Hinduism -
By T C Galav ISBN:
0964237709 p 17).
 Sir John Woodroffe,
(1865-1936) the well known scholar, Advocate-General of Bengal and sometime
Legal Member of the Government of India. He served with competence for eighteen
years and in 1915 officiated as Chief Justice. He has said: Sir John Woodroffe,
(1865-1936) the well known scholar, Advocate-General of Bengal and sometime
Legal Member of the Government of India. He served with competence for eighteen
years and in 1915 officiated as Chief Justice. He has said:
"Ages before Lamarck and Darwin it was held
in India that man has passed through 84 lakhs (8,400,000) of birth as plants,
animals, as an "inferior species of man" and then as the ancestor of
the developed type existing to-day.
"The theory was not,
like modern doctrine of evolution, based wholly on observation and a scientific
enquiry into fact but was a rather (as some other matters) an act of brilliant
intuition in which observation may also have had some part."
(source: Is
India Civilized: Essays on Indian Culture - By Sir John Woodroffe
Publisher: Ganesh & Co. Publishers Date of Publication: 1922 p. 22).
Thus, in Hinduism, science and religion are not
opposed fundamentally, as they often seem to be in
the West, but are seen as parts of the same great search for truth and enlightenment that
inspired the sages of Hinduism. Fundamental to Hindu concept of time and space is the
notion that the external world is a product of the creative play of Maya (illusion).

Kapila Rishi
To the philosophers of
India, however, Relativity is no new discovery, just as the concept of light
years is no matter for astonishment to people used to thinking of time in
millions of kalpas.
(image source: Vishwa
Hindu Parishad of America. Inc - 2002 calendar).
Refer
to Indian
Institute of Scientific Heritage
and Watch
Carl
Sagan and Hindu cosmology – video
***
"To the philosophers of
India, however, Relativity is no new discovery, just as the concept of light
years is no matter for astonishment to people used to thinking of time in
millions of kalpas, (A kalpa is about 4,320,000 years). The fact that the wise
men of India have not been concerned with technological applications of this
knowledge arises from the circumstance that technology is but one of innumerable
ways of applying it."
It is, indeed, a remarkable
circumstance that when Western civilization discovers Relativity it applies it
to the manufacture of atom-bombs, whereas Oriental civilization applies it to
the development of new states of consciousness."
(source: Spiritual
Practices of India - By Frederic Spiegelberg
Introduction by Alan Watts
p. 8-9).
 The late scientist,
Carl
Sagan,
asserts that the Dance
of Nataraja (Tandava)
signifies the cycle of evolution and destruction of the cosmic universe (Big
Bang Theory).
According to Carl Sagan, (1934-1996) astro-physicist, in his book
Cosmos says:
The late scientist,
Carl
Sagan,
asserts that the Dance
of Nataraja (Tandava)
signifies the cycle of evolution and destruction of the cosmic universe (Big
Bang Theory).
According to Carl Sagan, (1934-1996) astro-physicist, in his book
Cosmos says:
"The Hindu religion is the only one of the world's great
faiths dedicated to the idea that the Cosmos itself undergoes an immense, indeed an
infinite, number of deaths and rebirths. It is
the only religion in which the time scales correspond, to those of modern scientific
cosmology.
"It is the clearest image of the activity of God which any
art or religion can boast of." Modern physics has shown that the rhythm of
creation and destruction is not only manifest in the turn of the seasons and in
the birth and death of all living creatures, but also the very essence of
inorganic matter.
For modern physicists, then, Shiva's dance is the dance of subatomic matter.
Hundreds of years ago, Indian artist created visual images of dancing Shiva's in
a beautiful series of bronzes. Today, physicist have used the most advanced
technology to portray the pattern of the cosmic dance. Thus, the metaphor of the
cosmic dance unifies, ancient religious art and modern physics.
"The Hindu religion
is the only one of the world's great faiths dedicated to the idea that the
Cosmos itself undergoes an immense, indeed an infinite, number of deaths and
rebirths. It is the only religion in which
the time scales correspond, to those of modern scientific cosmology.
Its cycles run from our ordinary day and night to a day and night of Brahma,
8.64 billion years long. Longer than the age of the Earth or the Sun and about
half the time since the Big Bang. And there are much longer time scales
still."
(source: Cosmos
- By Carl Sagan ISBN: 0375508325 p. 213 -214). Watch
Carl
Sagan and Hindu cosmology – video
 Fritjof
Capra (1939 - )
Austrian-born famous theoretical high-energy physicist and ecologist wrote: Fritjof
Capra (1939 - )
Austrian-born famous theoretical high-energy physicist and ecologist wrote:
"Modern physics has thus revealed that every subatomic
particle not only performs an energy dance, but also is
an energy dance; a pulsating process of creation and destruction. The dance
of Shiva is the dancing universe, the ceaseless flow of energy going through an
infinite variety of patterns that melt into one another’’. For the modern physicists, then Shiva’s dance
is the dance of subatomic matter. As in Hindu mythology, it is a continual dance
of creation and destruction involving the whole cosmos; the basis of all
existence and of all natural phenomenon. Hundreds of years ago, Indian artists
created visual images of dancing Shivas in a beautiful series of bronzes. In our
times, physicists have used the most advanced technology to portray the patterns
of the cosmic dance."
(source: The
Tao of Physics: An Exploration of the Parallels Between Modern Physics and
Eastern Mysticism - By Fritjof Capra p.
241-245).
 Nancy
Wilson Ross (1901 -1986)
made her first trip to Japan, China, Korea and India in 1939. She
was the author
of several books including The World of Zen and
Time's Left Corner. Miss Ross lectured on Zen Buddhism at the Jungian
Institute in Zurich. She served on the board of the Asia Society
of New York which was founded by John D. Rockefeller III since
its founding in 1956 and was on the governing board of the India
Council. In private life she was known as Mrs. Stanley Young. Nancy
Wilson Ross (1901 -1986)
made her first trip to Japan, China, Korea and India in 1939. She
was the author
of several books including The World of Zen and
Time's Left Corner. Miss Ross lectured on Zen Buddhism at the Jungian
Institute in Zurich. She served on the board of the Asia Society
of New York which was founded by John D. Rockefeller III since
its founding in 1956 and was on the governing board of the India
Council. In private life she was known as Mrs. Stanley Young.
She
has written:
"Anachronistic as
this labyrinthine mythology may appear to the foreign mind, many
of India’s ancient theories about the universe are startlingly
modern in scope and worthy of a people who are credited with the
invention of the zero, as well as algebra and its application of
astronomy and geometry; a people who so carefully observed the
heavens that, in the opinion of Monier-Williams, they determined
the moon’s synodical revolution much more correctly than the
Greeks."
" Many hundreds of years before those
great European pioneers, Galileo and Copernicus, had to pay
heavy prices in ridicule and excommunication for their daring
theories, a section of the
Vedas known as the Brahmanas
contained this astounding statement:
“The sun never sets or rises. When people think the sun is
setting, he only changes about after reaching the end of the day
and makes night below and day to what is on the other side.
Then, when people think he rises in the morning, he only shifts
himself about after reaching the end of the day night, and makes day below and night to what is on the
other side. In truth, he does not see at all.”
"The Indians, whose theory of
time, is not linear like ours
– that is, not proceeding consecutively from past to present
to future – have always been able to accept, seemingly without
anxiety, the notion of an alternately expanding and contracting
universe, an idea recently advanced by certain Western
scientists. In Hindu cosmology, immutable Brahman, at fixed
intervals, draws back into his beginningless, endless Being the
whole substance of the living world. There then takes place the
long “sleep” of Brahaman from which, in course of countless
aeons, there is an awakening, and another universe or
“dream” emerges. "
"This notion of the
sleeping and waking, or contracting and expanding, of the Life
Force, so long a part of Hindu cosmology, has recently been
expressed in relevant terms in an article written for a British
scientific journal by Professor
Fred Hoyle, Britain’s foremost
astronomer. "

Lord
Vishnu sleeping on a coiled serpent. Chalukya Period. 6th century A.D.
Relief in
Sanctuary # 9, Aihole,
Lord
Vishnu is said to rest in the coils of Ananta, the great serpent of Infinity,
while he waits for the universe to recreate itself.
For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Refer
to Indian
Institute of Scientific Heritage
and Watch
Carl
Sagan and Hindu cosmology – video
***
"Plainly, contemporary Western science’s description of an
astronomical universe of such vast magnitude that distances must
be measured in terms as abstract as light-years is not new to
Hinduism whose wise men, millennia ago, came up with the term
kalpa to signify the inconceivable duration of the period
elapsing between the beginning and end of a world system.
"It is clear that Indian religious
cosmology is sharply at variance with that inherited by Western
peoples from the Semites.
On the highest level, when
stripped of mythological embroidery, Hinduism’s
conceptions of space, time and multiple universes approximate in
range and abstraction the most advanced scientific thought.
"
(source:
Three Ways of Asian Wisdom – By Nancy
Wilson Ross p. 64 - 67 and 74 - 76).
 Dr.
Heinrich Zimmer (1890-1943),
the great German Indologist, a man of penetrating intellect, the keenest
esthetic sensibility observed: Dr.
Heinrich Zimmer (1890-1943),
the great German Indologist, a man of penetrating intellect, the keenest
esthetic sensibility observed:
“In
one of the Puranic accounts of the deeds of
Vishnu in his Boar Incarnation or Avatar,
occurs a casual reference to the cyclic
recurrence of the great moments of myth. The Boar, carrying on his arm the
goddess Earth whom he is in the act of rescuing from the depths of the sea,
passingly remarks to her:
“Every
time I carry you this way….”
For
the Western mind, which believes in single, epoch-making, historical events
(such as, for instance, the coming of Christ) this casual comment of the ageless
god has a gently minimizing, annihilating effect."
(source:
The Myth and Symbols in India Art and Civilization –
By Heinrich Zimmer p. 18 and 152 - 155
).
 Professor Arthur Holmes
(1895-1965) geologist, professor at the University of Durham. He
writes regarding the age of the earth in his great book, The
Age of Earth (1913) as
follows: Professor Arthur Holmes
(1895-1965) geologist, professor at the University of Durham. He
writes regarding the age of the earth in his great book, The
Age of Earth (1913) as
follows:
"Long before it became a
scientific aspiration to estimate the age of the earth, many elaborate systems
of the world chronology had been devised by the sages of antiquity. The
most remarkable of these occult time-scales is that of the ancient Hindus, whose
astonishing concept of the Earth's duration has been traced back to Manusmriti,
a sacred book."
When the Hindu calculation of
the present age of the earth and the expanding universe could make Professor
Holmes so astonished, the precision with which the Hindu calculation regarding
the age of the entire Universe was made would make any man spellbound.
(source: Hinduism
and Scientific Quest - By T. R. R. Iyengar
p. 20-21).
The
Upanishads developed this spirit of inquiry, and traces of naturalistic and
scientific thought in them are quite significant. The Samkhya system, which has
been described as the ruling philosophy of pre-Buddhist India and an orthodox
system having its roots in the Upanishads, is essentially rational,
anti-theistic, and intellectual. According to
Richard Garbe, it was in Samkhya doctrine that complete independence and freedom
of the human mind was exhibited for the first time in history. Samkhya,
probably the oldest Indian philosophical system, furnished the background for
the Yoga system, and the early Buddhist biography Lalitavistara includes
both Samkhya and Yoga in the curriculum of study for the young Buddha. Samkhya
is generally ascribed to Sage Kapila and Yoga to Sage Patanjali. Ideas of natural selection, atomic polarity and
evolution.
Like in other ancient civilizations, in
Hindu India priests and scientists were often the same persons; the conflict
between religion and reason is not the primitive condition but a
contingent historical development in post-classical Europe, paralleled to an
extent by the stagnation of Muslim culture from the 12th century onwards. The Sankya philosophy of
Kapila, in short, is
devoted entirely to the systematic, logical, and scientific explanation of the
process of cosmic evolution from that primordial Prakriti, or eternal Energy.
There is no ancient philosophy in the world which was not indebted to the
sankhya system of Kapila. The idea of evolution which the ancient Greeks and
neo-Platonists had can be traced back to the influence of this Sankhya school of
thought.
(source: India
and World Civilization - By D. P. Singhal - Chapter V - Naturalism
and Science in Ancient India - p.153 - 188).
Professor Edward
Washburn Hopkins (1857-1932) Indologist, Chair of Sanskrit Studies of
Yale, says:
"Plato is full of Sankhyan thought, worked
out by him, but taken from Pythagoras. Before the sixth century B.C. all the
religious-philosophical idea of Pythagoras are current in India (L. Schroeder,
Pythagoras). If there were but one or two of these cases, they might be set
aside as accidental coincidences, but such coincidences are too numerous to be
the result of change. "
And
again he writes: "Neo-Platonism
and Christian Gnosticism owe much to India. The Gnostic ideas in regard to a
plurality of heavens and spiritual worlds go back directly to Hindu sources. Soul
and light are one in the Sankhyan system, before they became so in Greece, and
when they appear united in Greece it is by means of the thought which is
borrowed from India. The famous three qualities of the Sankhyan reappear as the
Gnostic 'three classes.'
(source:
Religions
of India - By Edward Washburn Hopkins
p. 559-560).
Some
sources even credit Pythagoras
with having traveled as far as India in search of knowledge, which
may explain some of the close parallels between Indian and Pythagorean
philosophy and religion. These parallels include:
- a
belief in the transmigration of souls;
- the
theory of four elements constituting matter;
- the
reasons for not eating beans;
- the
structure of the religio-philosophical character of the Pythagorean
fraternity, which resembled Buddhist monastic orders; and
- the
contents of the mystical speculations of the Pythagorean schools, which bear
a striking resemblance of the Hindu Upanishads.
According to Greek tradition,
Pythagoras, Thales, Empedocles, Anaxagoras, Democritus and others undertook
journey to the East to study philosophy and science. By the time
Ptolmaic Egypt and Rome’s Eastern empire had established themselves just
before the beginning of the Common era, Indian civilization was already well
developed, having founded three great religions – Hinduism, Buddhism and
Jainism – and expressed in writing some subtle currents of religious thought
and speculation as well as fundamental theories in science and medicine.
(source:
The
crest of the peacock: Non-European roots of Mathematics - By
George Gheverghese Joseph p.
1 - 18). For more refer to chapter on India
and Greece).
 A 9th century Hindu scripture, The Mahapurana
by Jinasena claims the something as modern as the following:
(translation from [5]) A 9th century Hindu scripture, The Mahapurana
by Jinasena claims the something as modern as the following:
(translation from [5])
"Some foolish men declare that a Creator made the world. The doctrine that
the world was created is ill-advised, and should be rejected. If God created the
world, where was he before creation?... How could God have made the world
without any raw material? If you say He made this first, and then the world, you
are faced with an endless regression... Know that the world is uncreated, as
time itself is, without beginning and end. And it is based on principles."
(source:
Astronomy
and Mathematics in Ancient India).
(Refer
to Visions
of the End of the World - By Dr. Subhash Kak - sulekha.com).
Modern
people divide the day into 24 hours, the hour - into 60 minutes, the minute -
into 60 seconds. Ancient Hindus divided the day in 60
periods, lasting 24 minutes each, and so on and so forth. The
shortest time period of ancient Hindus made up one-three-hundred-millionth of a
second.
(source: Ancient
nuclear blasts and levitating stones of Shivapur - By Alexander
Pechersky
- pravda.ru.com).
Speed
of Light:
Sayana
(c. 1315-1387) was a minister in the court of King
Bukka I of the Vijayanagar Empire in South India; he was also a great
Vedic scholar who wrote extensive commentaries on several ancient texts. In his
commentary on the fourth verse of the hymn 1.50 of the Rig
Veda on the sun, he says:
Tatha
cha smaryate yojananam sahasre dve dve shate dve cha yogane ekena nimishardhena
kramamana namo ‘stu ta iti
Thus
it is remembered: (O Sun), bow to you, you who travers 2,202 yojanas in half a
minute.
The
Puranas define 1 nimesha to be equal to 16/75 seconds. 1 yojana is about 9
miles. Substituting in Sayana’s statement we get 186,000 per second.
Sayana’s
statement was printed in 1890 in the famous edition of Rig Veda edited by Max
Muller, the German Sanskritist . He claimed to have used several three or four
hundred year old manuscripts of Sayana’s commentary, written much before the
time of Romer. Further support for the genuineness of the figure in the
ancient book comes from one of the earliest Puranas, the Vayu, conservatively
dated to at least 1,500 years old. The Puranas
speak of the creation and destruction of the universe in cycles of 8.64 billion
years, that is quite close to currently accepted value regarding the time of the
big bang.
(source:
The
Wishing Tree - By Subhash Kak p. 75 - 77 and Sayana's
Astronomy - By Subhash Kak).
Top
of Page
Physics
 In the realm of physics, remarkable contributions
have been made by Indian scientists.
Some hint at the theory may be contained in the views of Uddalaka
Aruni, preserved in the Chandogya Upanishad.
Uddalaka says: "matter was at first a chaotic mass, like the juices of
various trees indiscriminately blended together in honey. In order to develop
names-and-forms, to discriminate things from one another, or to set them in
order, the universal spirit came not in its universal form but as the living,
principle, and entered into Fire, Water and Earth. After separating their
component but qualitatively distinct parts (dhatus), it made numerous new
combinations of them. By propounding the theory of combination and separation of
particles, Uddalaka anticipated the atomic theory of Kannada.' In the realm of physics, remarkable contributions
have been made by Indian scientists.
Some hint at the theory may be contained in the views of Uddalaka
Aruni, preserved in the Chandogya Upanishad.
Uddalaka says: "matter was at first a chaotic mass, like the juices of
various trees indiscriminately blended together in honey. In order to develop
names-and-forms, to discriminate things from one another, or to set them in
order, the universal spirit came not in its universal form but as the living,
principle, and entered into Fire, Water and Earth. After separating their
component but qualitatively distinct parts (dhatus), it made numerous new
combinations of them. By propounding the theory of combination and separation of
particles, Uddalaka anticipated the atomic theory of Kannada.'
(image source: Vishwa
Hindu Parishad of America. Inc - 2002 calendar).
Kanaada,
the founder of the Vaisesika system of philosophy,
expounded that the entire matter in this world consists of atoms as many in kind
as the various elements. Kanaada's atom would then correspond to the modern atom.
He said:
"The cause of creative motion is believed to be adrsta, unseen moral
force which guides the destiny of souls according to their karma and requires
them to be provided with properly equipped bodies and an appropriate objective
world for the experience of pleasure and pain. It is due to the operation of
this metempirical force that atoms start moving to get together in order that
they may be integrated into countless varieties of things."
Some Jain thinkers went a step further. They thought that all atoms are the same
kind and variety emerged because they entered into different combinations.
Kanaada taught that light and heat are variations of the same reality.
Vacaspati
interpreted light as composed of minute particles emitted by substances and
striking the eyes. This is a clear anticipation of the corpuscular theory of
light, which was proposed by Newton but rejected till the discovery of the
proton.
Modern physics confirmed that the sun's rays
travel in a curved way, but not in a straight line. Our ancestors told that the
sun's chariot was drawn by seven horses tied by snakes. As the movements of the
snakes are crooked and curved, so also the sun's ray. The phenomenon is
described in a metaphysical poetic line bhujagana mita sapta turaga. The chapter
on light says that there are seven colors in the white ray of the sun.
Artharveda says that there are seven types of sun's rays, sapta surayasya
rasmayah.
The law of gravitation
discovered by Brahmagupta anticipated Newton by declaring "all
things fall to the earth by law of nature; for it is the nature of the earth to
attract and keep things."
(source:
Hinduism
and Scientific Quest - By T R. R. Iyengar p.
153-154 and History
of Science and Technology in Ancient India - by Debiprasad
Chattopadhya volume II p. 297-299). For
more information refer to the chapter 'Advanced
Concepts).
Kannada was an expounder of the law of causation
and of the atomic theory. He classified all the objects of creation into nine
elements, namely: earth, water, light, wind, ether, time, space, mind and soul.
According to his theory every object of creation is made of atoms, which in turn
are joined with each other to form molecules. His statement ushered in the
Atomic theory for the first time in the world, early 2500 years before John
Dalton. Kanaada has also described the dimension and motion of atoms and their
chemical reactions with each other.
T. N. Colebrooke,
has said: "Compared to the scientists of Europe, Kanaada and others Indian
scientists were the global masters in this field."
(source: Calendar 2002 -
VHP of America).
Umasvati, who
lived in the first century A.D. suggested that atoms of opposite qualities alone
combined and the atoms attracted or repelled as they were heterogeneous or
homogenous. Commenting on these theories, A. L Basham remarks: "Indian
atomic theories were not of course, based on experiment, but on intuition and
logic..."
Gravity was considered a peculiar cause of
primary descent or falling...In the absence of counter-balancing cause, as
adhesion, velocity or some act of volition, descent results from this quality.
Thus a coconut is withheld from falling by adhesion of the foot-stalk, but this
impediment ceasing on maturity of the fruit, it falls. The penetrative diffusion
of liquid was explained by capillary motion and the conduction of water in pipes
was said to be due to the pressure of air. They were familiar with an accurate
method of calculating velocity which facilitated the measurement of the relative
pitch of musical tones with great precision. They anticipated the Pythagorean
law of vibration of stretched strings. viz. the number of vibrations varies
inversely as the length of the string.
 The believed that energy was indestructible and
thus anticipated the law of conservation and energy. Heat and light were viewed
as only different forms of the same essential substance. One of the scientists
succeeded in suggesting a scientific explanation of the phenomenon of ebullition
and rarefaction in evaporation. They were familiar with refraction and chemical
effects of light rays, causes of translucency, opacity and shadows. They evolved
the formula that the angle of incidence was equal to the angle of reflection. The believed that energy was indestructible and
thus anticipated the law of conservation and energy. Heat and light were viewed
as only different forms of the same essential substance. One of the scientists
succeeded in suggesting a scientific explanation of the phenomenon of ebullition
and rarefaction in evaporation. They were familiar with refraction and chemical
effects of light rays, causes of translucency, opacity and shadows. They evolved
the formula that the angle of incidence was equal to the angle of reflection.
They discovered that a magnet possessed the power
of attracting iron. Bhoja, a writer of the
eleventh century, therefore, suggested that iron should not be used in the
construction of a ship to avoid the danger of being drawn into a magnetic field
by magnetic rocks. They also discovered the mariner's
compass centuries before its discovery in Europe. (for more
information refer to chapters War
in Ancient India and Seafaring
in Ancient India). It was called
matsya-yantra and consisted of an iron fish which floated in a vessel of oil and
pointed at the North.
(source: Main Currents
in Indian Culture - By S. Natarajan p. 68 - 69 Indo-Middle East
Cultural Studies Hyderabad 1960).
The
Indians came closest to modern ideas of atomism, quantum
physics, and other current theories. India developed
very early, enduring atomist theories of matter. Possibly Greek
atomistic thought was influenced by India, via the Persian
civilization. The Rig-Veda, is the
first Indian literature to set down ideas resembling universal
natural laws. Cosmic law is connected with cosmic light, with
gods, and, later, specifically with Brahman."
It was the Vedic Aryans... who gave
the world some of the earliest philosophical texts on the makeup
of matter and the theoretical underpinnings for the chemical
makeup of minerals. Sanskrit Vedas from thousands of years
before Christ implied that matter could not be created, and that
the universe had created itself. Reflecting this, in his Vaiseshika
philosophy, Kanada (600 B.
C) claimed that elements could not be destroyed. Kanada's life
is somewhat a mysterious, but his name is said to mean "one
who eats particle or grain" likely referring to his theory
that basic particles mix together as the building blocks for all
matter. Two, three, four, or more of these elements would
combine, just as we conceive of atoms doing. The Greeks would
not stumble on this concept for another century."
(source: Lost
Discoveries: The Ancient Roots of Modern Science - By Dick
Teresi p. 1 - 8 and 159 and 174 -239).
For more on Dick Teresi refer to chapters Quotes301_320,
GlimpsesVI and GlimpsesVII
).
Historian A. L. Basham
has written:
"The atomic theories of ancient India are
brilliant imaginative explanations of the physical structure of the
world..."
Further progress was made in knowing the
qualities and functions of earth, water, heat, sound etc. Especially in sound
the ancient Indians reached great heights very early. The octave was divided
into 22 shrutis (quarter-tones) and their proportions were measured with great
accuracy. Their love of accuracy and precision is testified by their tables of
weights, and measures. The measurement of time was, for example, based on the
unit of time taken by a wink (nimisha).
(source:
Ancient Indian History and Culture - By Chidambara
Kulkarni Orient Longman Ltd. 1974. p. 272).
J R Oppenheimer and Atom bomb
in modern times
 Only
seven years after the first successful atom bomb blast in New Mexico, Dr.
Oppenheimer of the Manhattan Project, who was
familiar with ancient Sanskrit literature, was giving a lecture at Rochester
University. During the question and answer period a student asked a question to
which Oppenheimer gave a strangely qualified answer: Only
seven years after the first successful atom bomb blast in New Mexico, Dr.
Oppenheimer of the Manhattan Project, who was
familiar with ancient Sanskrit literature, was giving a lecture at Rochester
University. During the question and answer period a student asked a question to
which Oppenheimer gave a strangely qualified answer:
Student: Was the bomb exploded at Alamogordo during the Manhattan Project the first one to
be detonated?
Dr. Oppenheimer: "Well -- yes. In modern times, of course.
Charles Berlitz
goes on to quote a number of passages from the Mahabharata that describe the
impact of a weapon that I suspect must be the brahmaastra, although he neither names
the weapon nor cites those sections of the text from which his quotations are drawn (he
lists Protap Chandra Roy's translation of 1889 in his bibliography):...a single projectile
Charged with all the power of the Universe.
An incandescent column of smoke and flame As bright as ten thousand Suns Rose in all its
splendor......it was an unknown weapon, An iron thunderbolt, A gigantic messenger of
death, Which reduced to ashes. The Entire race of the Vrishnis and the Andhakas....the
corpses were so burned As to be unrecognizable. Their hair and nails fell out; Pottery
broke without apparent cause, And the birds turned white. After a few hours all foodstuffs
were infected......To escape from this fire. The soldiers threw themselves in streams to
wash themselves and their equipment...
One is reminded of the yet
unknown final effect of a super-bomb when we read in the
Ramayana
of a
projectile:
...So powerful that it could
destroy
The earth in an instant -
A great soaring sound in smoke and flames...
And on it sits Death...
(source: Doomsday 1999
- By Charles Berlitz
Doubleday ASIN:
038515982X p. 118-122). For more on Oppenheimer, refer to
Quotes21_40
and GlimpsesX).
 Edward
Teller (1908-2003) was a Hungarian-born
American
theoretical physicist
who, although he claimed he did not care for the title, is known colloquially as
"the father of the hydrogen
bomb". Edward
Teller (1908-2003) was a Hungarian-born
American
theoretical physicist
who, although he claimed he did not care for the title, is known colloquially as
"the father of the hydrogen
bomb".
Lawrence Livermore National Laboratory, which Edward Teller help found, has
something in common with CERN's LHC. Both laboratories have a statue of the
Hindu god Shiva, which depicts this God performing a dance called the Nataraja
to destroy a weary universe in preparation to restart creation.
Teller
explained nuclear fusion in the following words:
“Laser lights
is brought in simultaneously from ten pipes on the top and ten pipes on the
bottom. Compression and nuclear reaction occurs in a tiny dot at the middle of
the sphere. Apparatus practically filling a whole building feeds the twenty
pipes, or the arms of the god Shiva. According to Hindu Creed, Shiva had three
eyes; two for seeing, and one (usually kept closed) to emit annihilating
radiation. The Hindus obviously know about lasers.”
(source:
Energy from Heaven and Earth – by Edward Teller p.
216 W H Freeman and Company. San Francisco 1979).
Top
of Page
Mathematics - The
Language of Science
“Like
the crest of a peacock, like the gem on the head of a snake, so is mathematics at
the head of all knowledge.”
– Vedanga
Jyotisa.
***
In mental abstraction and concentration of
thought the Hindus are proverbially happy. Apart from direct testimony on the
point, the literature of the Hindus furnishes unmistakable evidence to prove
that the ancient Hindus possessed astonishing power of memory and concentration
of thought. The science of mathematics, the most abstract of all sciences, must
have an irresistible fascination for the minds of the Hindus.
The great German critic, Schlegel
wrote in his History of Literature, p. 123:
"The decimal cyphers, the honor of which, next to letters the most
important of human discoveries, has, with the common consent of historical
authorities, been ascribed to Hindus."
Mathematics is the science to which Indians have
contributed the most. Our decimal system, place notation, numbers 1 through 9,
and the ubiquitous 0, are all major Indian contributions to world science.
Without them, our modern world of computer sciences, earth-launched satellites,
microchips, and artificial intelligence would all have been impossible.
(source:
An
Introduction to India - By Stanley Wolpert p. 194).
 Hermann
Hankel (1839 - 1873) born in Halle, Germany in his History
of Mathematics says: Hermann
Hankel (1839 - 1873) born in Halle, Germany in his History
of Mathematics says:
“ It is remarkable to what
extent Indian Mathematics enters into the Science of our time”
(source:
Is
India Civilized? - Essays on Indian Culture - By Sir John Woodroffe
Ganesh & Co. Publishers 1922 p. 182).
The earliest recorded Indian
mathematics was found along the banks of the Indus. Archaeologists have
uncovered several scales, instruments, and other measuring devices. The
Harappans employed a variety of plumb bobs that reveal a system of weights
27.584 grams. If we assign that a value of 1, other weights scale in at .05, .1,
.2, .5, 2, 5, 10, 20, 50, 100, 200 and 500. These weights have been found in
sites that span a five-thousand-year period, with little change in size.
Archaeologists also found a “ruler”
made of shell lines drawn 6.7 millimeters apart with a high
degree of accuracy. Two of the lines are distinguished by circles and
are separated by 33.5 millimeters, or 1.32 inches. This distance is the
so-called Indus inch.
(source:
Lost
Discoveries - Dick Teresi p.
59).
Dr.
David Gray writes:
"The
study of mathematics in the West has long been characterized by a
certain ethnocentric bias, a bias which most often manifests not
in explicit racism, but in a tendency toward undermining or
eliding the real contributions made by non-Western civilizations.
The debt owed by the West to other civilizations, and to India in
particular, go back to the earliest epoch of the
"Western" scientific tradition, the age of the classical
Greeks, and continued up until the dawn of the modern era, the
renaissance, when Europe was awakening from its dark ages."
Dr
Gray goes on to list some of the most important developments in
the history of mathematics that took place in India, summarizing
the contributions of luminaries such as Aryabhatta, Brahmagupta,
Mahavira, Bhaskara and Maadhava. He concludes by asserting that
"the role played by India in the
development (of the scientific revolution in Europe) is no mere
footnote, easily and inconsequentially swept under the rug of
Eurocentric bias. To do so is to distort history, and to deny
India one of its greatest contributions to world
civilization."
Mathematics
and Music:
Pingala
(3rd C AD), author of Chandasutra
explored the relationship between combinatorics and musical
theory anticipating Mersenne (1588-1648) author of a classic on
musical theory.
His contributions to mathematics include:
The formation of a matrix.
Invention of the binary number system (while he was forming a
matrix for musical purposes).
The concept of a binary code, similar to Morse
code.
First use of the Fibonacci
sequence.
First use of Pascal's
triangle, which he refers to as Meru-prastaara.
Used a dot (.) to denote zero.
His work, along with Panini's work, was foundational to the
development of computing.
(source: Science
and Mathematics in India). Refer to chapter on Hindu
Music and Indian
Mathematics.
Fascination
with numbers has been an abiding characteristic of Indian
civilization, not only large numbers but very small ones as well.
Operations with zero attracted the interest of both Bhaskaracharya
(b. 1114) and Srinivas Ramanujan (1887-1920).
 In
Ramayana, the great Indian
epic, there is a description of two armies facing, each other. The
size of
the larger army led by Rama is given as follows in a 17th
century translation of the epic by Kottayam Kerala varma
Thampuran: In
Ramayana, the great Indian
epic, there is a description of two armies facing, each other. The
size of
the larger army led by Rama is given as follows in a 17th
century translation of the epic by Kottayam Kerala varma
Thampuran:
Hundred
hundred thousands make a Crore
Hundred thousand crores make a Sankhu
Hundred thousand sankhus make a Maha-sankhu
Hundred thousand maha-sankhus make a Vriundam
Hundred thousand vriundam make a Maha-vriundam
Hundred thousand maha-vriundams make a Padmam
Hundred thousand padmams make a Maha-padmam
Hundred thousand maha-padmams make a Kharvam
Hundred thousand kharvams make a Maha-kharvam
Hundred thousand maha-kharvams make a Samudra
Hundred thousand samudras make a Maha-ougham.
The
importance of number names in the evolution of the decimal place
value notation in India cannot be exaggerated. The word-numeral
system was the logical outcome of proceeding by multiples of ten.
Thus, in an early system, 60,799 is denoted by the Sanskrit word
sastim (60), shsara (thousand), sapta (seven) satani (hundred),
navatim (nine ten times) and nava (nine). Such
a system presupposes a scientifically based vocabulary of number
names in which the principles of addition, subtraction and
multiplication are used. It requires:
- the
naming of the first nine digits (eka, dvi, tri, catur, pancha,
sat, sapta, asta, nava);
- a
second group of nine numbers obtained by multiplying each of
the nine digits in 1 by ten (dasa, vimsat, trimsat,
catvarimsat, panchasat, sasti, saptati, astiti, navati): and
- a
group of numbers which are increasing integral powers of 10,
starting with 102 (satam sagasara, ayut, niyuta,
prayuta, arbuda, nyarbuda, samudra, Madhya, anta, parardha…).
To
understand why word numerals persisted in India, even after the
Indian numerals became widespread, it is necessary to recognize
the importance of the oral mode of preserving and disseminating
knowledge. An important characteristic of written texts in India
from times immemorial was the sutra style of writing, which
presented information in a cryptic form, leaving out details and
rationale to be filled in by teachers and commentators. In short
pithy sentences, often expressed in verse, the sutras enabled the
reader to memorize the content easily.
(source:
The
crest of the peacock: Non-European roots of Mathematics - By
George Gheverghese Joseph p.401 - 403).
In the Vedic age, India was ahead of the rest in
mathematics and astronomy. Thus, the geometry of the Shulba
Sutras (The Rules of the Cord),
geometrical appendices to the manuals of ritual (Shrauta Sutras) include the
oldest known formulation of the theorem named after Pythagoras, developed in the
context of Vedic altar-building. The first decimal system and the oldest names
of "astronomical" numbers such as quadrillions and quintillions. Arabs
still call the decimal system rakmu 'l-Hind,
from Hind, "India."
(source: Mathematics
as Known to the Vedic Samhitas - By M. D. Pandit p. 20).
 Highly intellectual and given to abstract thinking as
they were, one would expect the ancient Indians to excel in mathematics. Ancient Indians developed a system of mathematics far
superior, to that of the Greeks. Ancient Vedic mathematicians devised sutras for
solving mathematical problems with apparent ease. Among the most vital parts of our heritage are
the numerals and the decimal system. The miscalled "Arabic" numerals
are found on the Rock Edicts of Ashoka (250 B.C.), a thousand years before their
occurrence in Arabic literature. Hindsaa
(numerals) in Arabic means from India. Jawaharlal Nehru has said, " The
clumsy method of using a counting frame and the use of Roman and such like
numerals had long retarded progress when the ten Indian numerals, including the
zero sign, liberated the human mind from these restrictions and threw a flood of
light on the behavior of numbers." Highly intellectual and given to abstract thinking as
they were, one would expect the ancient Indians to excel in mathematics. Ancient Indians developed a system of mathematics far
superior, to that of the Greeks. Ancient Vedic mathematicians devised sutras for
solving mathematical problems with apparent ease. Among the most vital parts of our heritage are
the numerals and the decimal system. The miscalled "Arabic" numerals
are found on the Rock Edicts of Ashoka (250 B.C.), a thousand years before their
occurrence in Arabic literature. Hindsaa
(numerals) in Arabic means from India. Jawaharlal Nehru has said, " The
clumsy method of using a counting frame and the use of Roman and such like
numerals had long retarded progress when the ten Indian numerals, including the
zero sign, liberated the human mind from these restrictions and threw a flood of
light on the behavior of numbers."
(source: The
Discovery of India - By Jawaharlal Nehru
Oxford University Press. 1995 p. 216).
Vedanga Jyotisa
says "As are the crests on the heads of peacocks, as are the gems on the
hoods of the snakes so is the ganita
(Mathematics) at the top of the sciences known as
Vedanga. In this period, ganita is a comprehensive term which
included arithmetic, algebra and astronomy. Geometry was also investigated but
was placed in a different general science known as kalpa. Indians were the first
to use the decimal either to increase or decrease the value of the figure which
was presided by Laplace, the great French mathematician. Indians were the first
to use the 'zero' as a symbol in mathematics. They invented the present
numerical system. India teachers taught arithmetic and algebra, Vedic Sulva
Sutras were earlier than the Alexandrian geometry of Hero. The earliest
available work was Bakshali Manuscript. Ganita-Sara-Sangraham
of Mahavira acarya who lived between Brahmagupta and Bhaskaracharya.
The 'Pythagoras theorem' which stated in Sulva
Sutras by Baudhayana's (6th century C.
E): "The diagonal of a rectangle
produces both areas, which its length and breadth produce separately." Arya
Bhatta discovered the method of finding out the areas of a triangle, a trapezium
and a circle. The approximate value of an 'irrational number' i.e. 2 (dvikarani)
(1.143256) and 3 (1.7320513) can be obtained, Baudhayana and Apastamba.
In the geometry of the circle, "Arybhatta
I" gave a value for pi (tyajya) which is correct to the four decimal places
in a sloka (Sankara Varman's treatise on astronomy, Sadratnamala) theorems and
their deductions:
"Lemma of Brahmagupta for integral solution
or the indeterminate equation of second degree. John
Pell (1611-1685) discovered this in the
17th century. Indians discovered it a 1,000 years earlier.
(source:
Hinduism
and Scientific Quest - By T R. R. Iyengar p.
151-152).
The most fundamental contribution of ancient
India in mathematics is the invention of decimal system of enumeration,
including the invention of zero. The decimal system uses nine digits (1 to 9)
and the symbol zero (for nothing) to denote all natural numbers by assigning a
place value to the digits. The Arabs carried this system to Africa and Europe. The
Vedas and Valmiki Ramayana used this system, though the exact
dates of these works are not known. MohanjoDaro and Harappa excavations (which
may be around 3000 B.C. old) also give specimens of writing in India. Aryans
came 1000 years later, around 2000 B.C. Being very religious people, they were
deeply interested in planetary positions to calculate auspicious times, and they
developed astronomy and mathematics towards this end. They identified various nakshatras
(constellations) and named the months after them. They could count up to 1012,
while the Greeks could count up to 104 and Romans up to 108.
Values of irrational numbers were
also known to them to a high degree of approximation. Pythagoras Theorem can be
also traced to the Aryan's Sulbasutras. These Sutras, estimated to be
between 800 B.C. and 500 B.C., cover a large number of geometric principles.
 Said the great and magnanimous Pierre Simon de
Laplace, (1749-1827) French mathematician, philosopher,
and astronomer, a contemporary of Napoleon :
Said the great and magnanimous Pierre Simon de
Laplace, (1749-1827) French mathematician, philosopher,
and astronomer, a contemporary of Napoleon :
" It is India that gave us the ingenious method
of expressing all numbers by ten symbols, each receiving a value of position as
well as an absolute value, a profound and important idea which appears so simple
to us now that we ignore its true merit. But its very simplicity, the great ease
which it has lent to all computations, puts our arithmetic in the first rank of
useful inventions, and we shall appreciate the grandeur of this achievement the
more when we remember that it escaped the genius of Archimedes and Appollnius,
two of the greatest men produced by antiquity."
(source:
The
Discovery of India - By Jawaharlal Nehru
Oxford University Press. 1995 p. 217).
Brilliant as it was, this invention was no accident. In the
Western world, the cumbersome Roman numeral system posed as a major obstacle,
and in China the pictorial script posed as a hindrance. But in India, almost
everything was in place to favor such a development. There was already a long
and established history in the use of decimal numbers, and philosophical and
cosmological constructs encouraged a creative and expansive approach to number
theory. Panini's studies in linguistic theory and formal language and the
powerful role of symbolism and representational abstraction in art and
architecture may have also provided an impetus, as might have the rationalist
doctrines and the exacting epistemology of the Nyaya Sutras, and the innovative
abstractions of the Syadavada and Buddhist schools of learning.
Panini and Formal Scientific
Notation
A
particularly important development in the history of Indian
science that was to have a profound impact on all mathematical
treatises that followed was the pioneering work by Panini
(6th C BC) in the field of Sanskrit grammar and linguistics.
Besides expounding a comprehensive and scientific theory of
phonetics, phonology and morphology, Panini provided formal
production rules and definitions describing Sanskrit grammar in
his treatise called Asthadhyayi. Basic elements such as vowels and
consonants, parts of speech such as nouns and verbs were placed in
classes. The construction of compound words and sentences was
elaborated through ordered rules operating on underlying
structures in a manner similar to formal language theory.
Today,
Panini's constructions can also be seen as comparable to modern
definitions of a mathematical function. G G Joseph, in The crest
of the peacock argues that the algebraic nature of Indian
mathematics arises as a consequence of the structure of the
Sanskrit language. Ingerman in his paper titled Panini-Backus form
finds Panini's notation to be equivalent in its power to that of
Backus - inventor of the Backus
Naur Form used to describe the syntax of modern
computer languages. Thus Panini's work provided an example of a
scientific notational model that could have propelled later
mathematicians to use abstract notations in characterizing
algebraic equations and presenting algebraic theorems and results
in a scientific format.
(source: Science
and Mathematics in India).
 John
D Barrow (1952 - )
is an English cosmologist
theoretical physicist
and mathematician.
He is currently Research Professor of Mathematical Sciences at the University
of Cambridge. John
D Barrow (1952 - )
is an English cosmologist
theoretical physicist
and mathematician.
He is currently Research Professor of Mathematical Sciences at the University
of Cambridge.
In his book,
Pi in the Sky: Counting, thinking and Being he has observed:
“The Indian system of counting has
been the most successful intellectual innovation ever made on our planet. It has
spread and been adopted almost universally, far more extensively, even than the
letters of the Phoenician alphabet which we now employ. It constitutes the
nearest thing we have to a universal language,”
(source:
Pi in the Sky: Counting, thinking and Being - by John D Barrow p.
92).
The decimal system was known to Aryabhatta and
Brahmagupta long before its appearance in the writings of the Arabs and the
Syrians; it was adopted by China from Buddhist missionaries; and Muhammad Ibn
Musa al-Khwarazni, the greatest mathematician of his age (ca 850 A.D.), seems to
have introduced it into Baghdad.
Zero, this most modest and most valuable
of all numerals is one of the subtle gifts of India to mankind.
The
earliest use of the zero symbol, so far discovered, is in one of the scriptural
books dated about 200 B.C. The zero, called shunya or nothing, was
originally a dot and later it became a small circle. It was considered as a
number like any other. Professor G. B. Halsted,
in his book ' Mathematics for the Million'
(London 1942)
thus emphasizes the vital significance of this
invention:
"The importance of the creation of the zero mark can never be exaggerated.
This giving to airy nothing, not merely a local habitation and a name, a
picture, a symbol but helpful power, is the characteristic of the Hindu race
whence it sprang. It is like coining the Nirvana into dynamos. No single
mathematical creation has been more potent for the general on-go of intelligence
and power." It was India that first domesticated zero, through the Hindu
familiarity with the concepts of infinity and the void. Neither pagan Rome nor
the Christian Europe of the Middle Ages had any truck with it. It's all, as the
Hindus knew, a play between the void and the absolute.
Yet another modern mathematician has grown eloquent
over this historic event. Dantzig
in his 'Number' writes:
"This long period of nearly five thousand years saw the rise and fall of
many a civilization, each leaving behind a heritage of literature, art,
philosophy, and religion. But what was the net achievement in the field of
reckoning, the earliest art practiced by man? An inflexible numeration so crude
as to make progress well nigh impossible, and a calculating device so limited in
scope that even elementary calculations called for the services of an
expert.....When viewed in this light the achievements of the unknown Hindu, who
sometime in the first centuries of our era discovered the principle of position,
assumes the importance of a world event."
Dantzig is puzzled at the fact that the great
mathematicians of Greece did not stumble on this discovery.
"Is it that the Greeks had such a marked contempt for applied
science, leaving even the instruction of their children to the slaves? But if
so, how is it that the nation that gave us geometry and carried this science so
far did not create a rudimentary algebra? that corner-stone of modern
mathematics, also originated in India, and at about the same time that
positional numeration did?"
(source:
The
Discovery of India - By Jawaharlal Nehru
Oxford University Press. 1995 p. 218)
The Unsung Mathematician:
An important Mathematics book prescribed by the New York State Education
Department acknowledges the debt in the following words:
 "The Western world owes
a great deal to India for a simple invention. It was developed by an unknown
Indian more than 1500 years ago. Without it most of the great discoveries and
inventions (including computers) of western civilization would never have come
about. This invention was the decimal system of numerals - nine digits and a
zero. The science and technology of today (including the computers) could not
have developed if we had only the Roman system of numerals. That system is too
clumsy to be used as a scientific too. Today we take the decimal system for
granted. We don't think about how brilliant the man who invented zero must have
been. Yet without zero we could not assign a place value to the digits. That
ancient mathematician, whoever, he was, deserves much honor." "The Western world owes
a great deal to India for a simple invention. It was developed by an unknown
Indian more than 1500 years ago. Without it most of the great discoveries and
inventions (including computers) of western civilization would never have come
about. This invention was the decimal system of numerals - nine digits and a
zero. The science and technology of today (including the computers) could not
have developed if we had only the Roman system of numerals. That system is too
clumsy to be used as a scientific too. Today we take the decimal system for
granted. We don't think about how brilliant the man who invented zero must have
been. Yet without zero we could not assign a place value to the digits. That
ancient mathematician, whoever, he was, deserves much honor."
Indians also made advances in other areas of mathematics.
Very early in their history they developed a simple system of geometry. This
system was used to plan outdoor sites for Indian religious ceremonies. Indians
also added to our knowledge of even more complicated branches of mathematics
such as trigonometry and calculus. They studied these branches of mathematics in
order to apply them to astronomy."
(source:
Harry Shor and Gloria Meng, Exploring
Algebra).
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju.
Refer to
Visualizing
Indian heritage Digital Library Metaphor
– By
Nagnath R Ramdasi - CDAC.
 Charles Seife, a journalist with Science
magazine, has also written for New Scientist, Scientific American, The Economist,
Science, Wired UK, The Sciences, and
numerous other publications. He holds an M.S. in mathematics from Yale
University and his areas of research include probability theory and artificial
intelligence. He is a
mathematician and science writer, author of
Zero: The
Biography of a Dangerous Idea
says:
Charles Seife, a journalist with Science
magazine, has also written for New Scientist, Scientific American, The Economist,
Science, Wired UK, The Sciences, and
numerous other publications. He holds an M.S. in mathematics from Yale
University and his areas of research include probability theory and artificial
intelligence. He is a
mathematician and science writer, author of
Zero: The
Biography of a Dangerous Idea
says:
"Perhaps no one has embraced nothing as strongly
as the Indians who, Seife notes, "never had a fear of the infinite or of
the void." Hinduism has embedded within it, a complex philosophy of
nothingness, seeing everything in the world as arising from the pregnant void,
known as Sunya.
"The ultimate goal of the Hindu was to free
himself from the endless cycle of pain found in continual reincarnation and
reconnect with the Nothingness that is the source and fundament of the All.
For Indians, the void of Sunya was the very font of all potential; nothingness
was liberation. No surprise then that it is from this sophisticated culture that
we inherit the mathematical analog of nothing, zero. Like Sunya, zero is a kind
of place holder, a symbol signifying a pregnant space where any other number
might potentially reside."
(source: Zero: The Biography of a Dangerous Idea:
It's weird, it's counterintuitive and the Greeks hated it. Why did the Church
reject the use of zero?
http://www.calendarlive.com/top/1,1419,L-LATimes-Books-X!ArticleDetail-26133,00.html
http://www.salon.com/books/review/2000/03/03/seife/index.html).
Lancelot Thomas Hogben
(1895-1975) English zoologist and geneticist, has written:
"In the whole history of Mathematics, there has been no more revolutionary step
than the one which the Hindus made when they invented the sign ‘0’ for the
empty column of the counting frame."
(source:
Mathematics
for the Million - By Lancelot
Thomas Hogben p. 47).
The concept of Debits and negative numbers
originated in India, and why were they not accepted until recently? It was much
more than 2000 years ago. It wasn't accepted elsewhere because the Church did
not think it possible.
The paper of Reuben
Burrow (1798-1868) "A Proof that
the Hindus had the Binomial Theorem." (published in 1790) Asiatic
Researches 2 (1790): 487-97 is more proof for us that the western world was
aware of the Indian achievement in the field of combinational mathematics. Then,
the problem would be one of explaining how the so called 'Pascal's triangle'
continues to bear his name, or how the British reference books like the
Encyclopedia Britannica persisted (till well into the 20th century) in crediting
Newton with the discovery of the binomial theorem.
(source: India
Through The Ages: History, Art Culture and Religion - By G. Kuppuram
p. 672-673).
The Hindus knew mathematics much early. In the Rig
Veda (2-18, 4 to 6), there are references to ‘two’, ‘four’,
‘eight’, ‘ten.’
Aa dvabhyam haribhyamindryahya
chaturbhirashadabhi rhuya manah ashtabhirdashabhih
Also in Vajasaneya Samhita
(17.2), there is the passage referring to 1, 10, 100, 1000 etc.
Eka cha dasha cha dasha cha shatam cha shatam cha
sahasram cha sahasram cha yutam cha ayutam cha
niyutam cha niyutam cha prayutam cha. Etc.
In Mahabharata there are
references to addition and subtraction. Adhikam (more), Unam (less), Shesham
(remaining), multiplication and division are indicated. For example, “60
thousand camels and twice the number of horses” are referred to.
 In Rig Veda (10.62.7), Nabhanedishta praises King Savarni for
giving in charity one thousand cows, who had the figure 8 on their ears and so
were called Ashta Karni. It seems that gambling was very common in the Vedic
days, and it involved dices and numbers. According to Yajur Veda, Vajasneya
Samhita (4.3,3), in the Rajasuya sacrifice, five was called Abhiburasi. In
another kind of gambling, the dice (Aksha) used four names of the four Ages
namely Krita, Treta, Dvapar and Kali and they were numbered 4, 3, 2 and 1. The
numbers from one to one thousand billion are found in the Vajasneya
Samhita and also in Taitteriya, Maitrayani and Kathaka Samhitas. In Rig Veda (10.62.7), Nabhanedishta praises King Savarni for
giving in charity one thousand cows, who had the figure 8 on their ears and so
were called Ashta Karni. It seems that gambling was very common in the Vedic
days, and it involved dices and numbers. According to Yajur Veda, Vajasneya
Samhita (4.3,3), in the Rajasuya sacrifice, five was called Abhiburasi. In
another kind of gambling, the dice (Aksha) used four names of the four Ages
namely Krita, Treta, Dvapar and Kali and they were numbered 4, 3, 2 and 1. The
numbers from one to one thousand billion are found in the Vajasneya
Samhita and also in Taitteriya, Maitrayani and Kathaka Samhitas.
In Sama Veda, in the 25th
Brahmana, there is a reference to how much fees (dakshina) should be given to a
priest in sacrifice (Yajna). It may be at least 12 (Krishnala) milligrams of
gold, and doubling the figure, it can go up to 3,93,216.
The system they adopt in giving page numbers in old
manuscripts in Malabar and in Andhra was to have 34 digits of consonants from Ka
to La and then to have the next 34 digits by adding vowels Kaa to Laa. They can
number pages upto 408 (34 x 12).
Burma also had the same system for pagination.
(source:
Hinduism: Its Contribution to Science and Civilization
- By Prabhakar Balvant Machwe p. 10 -14).
The Notion of Infinity and zero:
There is a beautiful definition of the infinite
in the following line of a Vedic mantra, which forms the introductory verse to
the Isa Upanishad:
It says: Take the whole (Infinite Brahman) from
the whole, and the whole still remains. This is almost like the mathematician,
Cantor's definition of infinity.
The very names of the numerals are of Sanskrit
origin. Professor Arthur Macdonell says in
his A
History of Sanskrit Literature: "During the eighth and ninth
centuries, the Indians became the teachers in arithmetic and algebra of the
Arabs, and through them of the nations of the west. Thus, though we call the
latter science by an Arabic name, it is a gift we owe
to India."
(source: Indian Culture
and the Modern Age - By Dewan Bahadur K. S. Ramaswami Sastri
Annamalai University. 1956 p.66-67).
The linkage of God with the infinite is found in the Bhagavad
Gita, by tradition spoken by Lord Krishna himself, we
read:
“O Lord of the universe, I see You
everywhere with infinite form…Neither do I see the beginning nor
the middle nor the end of Your Universal Form.”
(source: Infinity:
The Quest to Think the Unthinkable - By Brian Clegg p. 54).
Refer to
Sciences of the Ancient Hindus: Unlocking Nature in
the Pursuit of Salvation – By Alok Kumar
Zero
to Infinity in Indian Mysticism
Ananta
is Sanskrit for infinity. It is equated with the
Supreme Brahman — infinitely powerful and so infinitely free. It is bigger
than any quantity that can be imagined; it is bigger than any finite number.
Infinity is one of the fundamental axioms upon which contemporary mathematics is
based.
Sanskrit grammar
and interpretation in ancient India were closely linked to the handling of high
value numbers. Studies relating to poetry and metrics initiated sastragnaas or
scientists to both arithmetic and grammar. Grammarians were just as competent at
calculations as professional mathematicians. Indian sastragnaas or scientists,
philosophers, astronomers and cosmographers — in order to develop their
arithmetical, metaphysical and cosmological speculations concerning ever higher
numbers — became at once mathematicians, grammarians and poets. They gave
their spoken counting system a truly mathematical structure which had the
potential to lead directly to the discovery of the decimal place-value system.
 In
Indian mysticism, the concept of infinity and zero are very closely linked. In
the Isavasya
Upanishad,
there’s a line: “Poornasya poornam aadaya poornameva visish-yate”. To
mathematically explain this, we have to assume that the first poornam represents
infinity and the second, zero.
In Sanskrit, poornam means both full and zero. Indian mathematicians knew
perfectly well how to distinguish between these two notions which are mutually
contradictory and which are the inverse of each other. They knew that division
by zero gave them infinity. The concept of infinity has
always remained an enigma. The Taittiriya Upanishad says: yatho vacho nivartante,
apraapya manasa saha — where mind and speech return (being) unable to
comprehend. In Indian cosmology, Ananta refers to the Adisesha or the great
serpent on which Lord Vishnu reclines, taking His yoga nidra or anantasayanam. In
Indian mysticism, the concept of infinity and zero are very closely linked. In
the Isavasya
Upanishad,
there’s a line: “Poornasya poornam aadaya poornameva visish-yate”. To
mathematically explain this, we have to assume that the first poornam represents
infinity and the second, zero.
In Sanskrit, poornam means both full and zero. Indian mathematicians knew
perfectly well how to distinguish between these two notions which are mutually
contradictory and which are the inverse of each other. They knew that division
by zero gave them infinity. The concept of infinity has
always remained an enigma. The Taittiriya Upanishad says: yatho vacho nivartante,
apraapya manasa saha — where mind and speech return (being) unable to
comprehend. In Indian cosmology, Ananta refers to the Adisesha or the great
serpent on which Lord Vishnu reclines, taking His yoga nidra or anantasayanam.
The
symbol for infinity is called the leminiscate. English mathematician John Wallis
introduced this symbol for the first time in 1655. Hindu mythological
iconography contains a similar symbol representing the same idea. The symbol is
that of Ananta, the great Adisesha of infinity and eternity, which is always
represented, coiled up in a horizontal figure of 8 just like the leminiscate.
Negative
numbers had been rejected as solutions of problems in early times. They were
eventually admitted in Hindu practical mathematics through problems involving
money transactions, since the idea of receiving and owing money was a simple and
obvious one — a negative number could be interpreted as a debt. Objection to
negative numbers continued up to the early 19th century. Negative numbers are
the mirror image of positive numbers. The invention of Cartesian geometry
brought the X, Y co-ordinates and numbers came to be represented on a graph.
Today, the series of negative natural numbers go up to infinity.
(source:
Zero
to Infinity in Indian Mysticism - By T
R Rajagopalan
- Times of India).
‘Calculus
is
India
’s Gift to
Europe
’
 Dr.
C.K. Raju
(1954 - ) holds
a Ph.D. from the Indian Statistical Institute. He taught
mathematics for several years before playing a lead role in the C-DAC
team which built Param:
India
’s first parallel supercomputer. His earlier book ‘Time:
Towards a Consistent Theory’ (Kluwer Academic, 1994) set out a
new physics with a tilt in the arrow of time. He has been a Fellow
of the Indian Institute of Advanced Study and is a Professor of
Computer Applications. Dr.
C.K. Raju
(1954 - ) holds
a Ph.D. from the Indian Statistical Institute. He taught
mathematics for several years before playing a lead role in the C-DAC
team which built Param:
India
’s first parallel supercomputer. His earlier book ‘Time:
Towards a Consistent Theory’ (Kluwer Academic, 1994) set out a
new physics with a tilt in the arrow of time. He has been a Fellow
of the Indian Institute of Advanced Study and is a Professor of
Computer Applications.
He
has has revealed how calculus, an Indian invention, was
picked up by the Jesuit priests from Kerala in the second half of
the 16th century and taken to Europe. This is how the Westerners
got their calculus. Overtime, people forgot this link and the
Europeans began to claim calculus as their own invention. This
myth still persists despite calculus texts existing in
India
since thousands of years.
“Indian
infinite series has been known to British scholars since at least
1832, but no scholar tried to establish the connection with the
calculus attributed to
Newton
and Leibnitz,” he said.
Dr. Raju’s
10-year research that included archival work in Kerala and
Rome
was published in a book “Cultural Foundations of Mathematics.”
It established that the Jesuit priests took trigonometric tables
and planetary models from the Kerala mathematicians of the
Aryabhata school and exported them to
Europe
starting around 1560 in connection with the European navigational
problem.
“When
the Europeans received the Indian calculus, they couldn’t understand it
properly because the Indian philosophy of mathematics is different from the
Western philosophy of mathematics. It took them about 300 years to fully
comprehend its working. The calculus was used by
Newton
to develop his laws of physics,”
It
is well known that the “Taylor-series” expansion, that is at
the heart of calculus, existed in
India
in widely distributed mathematics / astronomy / timekeeping (“jyotisa”)
texts which preceded
Newton
and Leibniz by centuries.
Why were
these texts imported into
Europe
? These texts, and the accompanying precise sine values computed
using the series expansions, were useful for the science that was
at that time most critical to
Europe
: navigation. The ‘jyotisa’ texts were specifically needed by
Europeans for the problem of determining the three “ells”:
latitude, loxodrome, and longitude.
How were
these Indian texts imported
into
Europe
? Jesuit records show that they sought out these texts as inputs
to the Gregorian calendar reform. This reform was needed to solve
the ‘latitude problem’ of European navigation. The Jesuits
were equipped with the knowledge of local languages as well as
mathematics and astronomy that were required to understand these
Indian texts.
 The
Jesuits also needed these texts to understand the local
customs and how the dates of traditional festivals were fixed by
Indians using the local calendar (“panchânga”). How the
mathematics given in these Indian ancient texts subsequently
diffused into
Europe
(e.g. through clearing houses like Mersenne and the works of
Cavalieri, Fermat, Pascal, Wallis, Gregory, etc.) is yet another
story. The
Jesuits also needed these texts to understand the local
customs and how the dates of traditional festivals were fixed by
Indians using the local calendar (“panchânga”). How the
mathematics given in these Indian ancient texts subsequently
diffused into
Europe
(e.g. through clearing houses like Mersenne and the works of
Cavalieri, Fermat, Pascal, Wallis, Gregory, etc.) is yet another
story.
The calculus
has played a key role in the development of the sciences, starting
from the “Newtonian Revolution”. According to the
“standard” story, the calculus was invented independently by
Leibniz and
Newton
. This story of indigenous development, ab initio, is now
beginning to totter, like the story of the “Copernican
Revolution”.
The
English-speaking world has known for over one and a half centuries
that “Taylor series” expansions for sine, cosine and
arctangent functions were found in Indian mathematics / astronomy
/ timekeeping (‘jyotisa’) texts, and specifically in the works
of Madhava, Neelkantha, Jyeshtadeva, etc. No one else,
however, has so far studied the connection of these Indian
developments to European mathematics.
The connection
is provided by the requirements of the European navigational
problem, the foremost problem of the time in
Europe
. Columbus and Vasco da Gama used dead reckoning and were ignorant
of celestial navigation. Navigation, however, was both
strategically and economically the key to the prosperity of
Europe
of that time.
Jesuits such
as Matteo Ricci who trained in
mathematics and astronomy under Clavius’ new syllabus were sent
to
India
. In a 1581 letter, Ricci explicitly
acknowledged that he was trying to understand the local methods of
time-keeping (‘jyotisa’)
from the Brahmins and Moors in the vicinity of
Cochin
.
Cochin
was then the key centre for mathematics and
astronomy since the Vijaynagar Empire
had sheltered it from the continuous onslaughts of Islamic raiders
from the north. Language was not a problem for the Jesuits since
they had established a substantial presence in
India
.
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju.
(source: ‘Calculus
is
India
’s Gift to
Europe
’ - By Dr. C K Raju - indianrealist.com).
In his speech introducing the Indian Budget March
1st, 1926, Sir Basil Blackett said:
"India long ago revolutionized mathematics,
and provided the West with the key to the most far reaching of all the
mechanical instrument on which its control of nature has been built, when it
presented to Europe through the medium of Arabia the device of the cypher (and
the decimal notation) upon which all modern system of numeration depend. even
so, India today or tomorrow, will, I am confident, revolutionize western
doctrines of progress by demonstrating the insufficiency and lack of finality of
much of the West's present system of human values."
(source: India
in Bondage: Her Right to Freedom - Rev. Jabez T. Sunderland
p.356-357).
Georges
Ifrah ( ? ) French
historian of Mathematics and author of the book, The
Universal History of Numbers has written:
"The
Indian mind has always had for calculations and the handling of
numbers an extraordinary inclination, ease and power, such as no
other civilization in history ever possessed to the same degree.
So much so that Indian culture regarded the science of numbers
as the noblest of its arts...A thousand years ahead of
Europeans, Indian savants knew that the zero and infinity were
mutually inverse notions."
(source:
Histoire
Universelle des Chiffres - By Georges Ifrah
Paris - Robert Laffont, 1994, volume 2. p. 3).
“The real inventors of [the numeral system], which is no
less important than such feats as the mastery of fire, the development of
agriculture, or the invention of the wheel, writing or the steam engine, were
the mathematicians and astronomers of Indian
civilization: scholars who, unlike the Greeks, were concerned with
practical applications and who were motivated by a kind of passion for both
numbers and numerical calculations.”
 Claiming
India to be the true birthplace of our numerals, Ifrah salutes the Indian
researchers saying that the "...real inventors of this
fundamental discovery, which is no less important than such
feats as the mastery of fire, the development of agriculture, or
the invention of the wheel, writing or the steam engine, were
the mathematicians and astronomers of the Indian civilization:
scholars who, unlike the Greeks, were concerned with practical
applications and who were motivated by a kind of passion for
both numbers and numerical calculations." Claiming
India to be the true birthplace of our numerals, Ifrah salutes the Indian
researchers saying that the "...real inventors of this
fundamental discovery, which is no less important than such
feats as the mastery of fire, the development of agriculture, or
the invention of the wheel, writing or the steam engine, were
the mathematicians and astronomers of the Indian civilization:
scholars who, unlike the Greeks, were concerned with practical
applications and who were motivated by a kind of passion for
both numbers and numerical calculations."
He
refers to 24 evidences from scriptures from India, whose dates
range from 1150 BC until 458 BC. Of particular interest is the
work by Indian mathematician Bhaskaracharya
known as Bhaskara (1150 BC) where he makes a reference to zero
and the place-value system were invented by the god Brahma.
In other words, these notions were so well established in
Indian thought and tradition that at this time they were
considered to have always been used by humans, and thus to have
constituted a "revelation" of
the divinities.
"It
was only after the eighth century BC, and doubtless due to the
influence of the Indian Buddhist missionaries, that Chinese
mathematicians introduced the use of zero in the form of a
little circle or dot (signs that originated in India),...".
The
early passion which Indian civilization had for high numbers was
a significant factor contributing to the discovery of the
place-value system, and not only offered the Indians the
incentive to go beyond the "calculable" physical
world, but also led to an understanding (much earlier than in
our civilization) of the notion of mathematical infinity itself.
Sanskrit
notation had an excellent conceptual quality. It was easy to use
and moreover it facilitated the conception of the highest
imaginable numbers. This is why it was so well suited to the
most exuberant numerical or arithmetical-cosmogonic speculations
of Indian culture."
"The
Indian people were the only civilization to take the decisive
step towards the perfection of numerical notation. We owe the
discovery of modern numeration and the elaboration of the very
foundations of written calculations to India alone."
"It is clear how
much we owe to this brilliant civilization, and not only in the
field of arithmetic; by opening the way to the generalization of
the concept of the number, the Indian scholars enabled the rapid
development of mathematics and exact sciences. The discoveries
of these men doubtless required much time and imagination, and
above all a great ability for abstract thinking. These
major discoveries took place within an environment which was at
once mystical, philosophical, religious, cosmological,
mythological and metaphysical."
"In India,
an aptitude for the study of numbers and arithmetical research
was often combined with a surprising tendency towards metaphysical
abstractions; in fact,
the latter is so deeply ingrained in Indian thought and
tradition that one meets it in all fields of study, from the
most advanced mathematical ideas to disciplines completely
unrelated to 'exact sciences.
In
short, Indian science was born out of a mystical and religious
culture and the etymology of the Sanskrit words used to describe
numbers and the science of numbers bears witness to this fact.
"
"Sanskrit means “complete”, “perfect” and
“definitive”. In fact, this language is extremely
elaborate, almost artificial, and is capable of
describing multiple levels of
meditation, states of consciousness and psychic, spiritual and
even intellectual processes. As for vocabulary, its
richness is considerable and highly diversified. Sanskrit has
for centuries lent itself admirably to the diverse rules of
prosody and versification. Thus we can see why poetry has played
such a preponderant role in all of Indian culture and Sanskrit
literature.
"
(source:
The
Universal History of Numbers - By Georges
Ifrah p 365 - 441).
 Marcus
du Sautoy (1965 -
) is a Professor of Mathematics at University
of
Oxford. Formerly of
All
Souls
College, he is now a fellow of
Wadham
College. He has been named by The
Independent on Sunday as one of the
UK
's leading scientists. In 2001 he won the prestigious Berwick
Prize of the London Mathematical Society, which is awarded every
two years to reward the best mathematical research by a
mathematician under forty. Marcus
du Sautoy (1965 -
) is a Professor of Mathematics at University
of
Oxford. Formerly of
All
Souls
College, he is now a fellow of
Wadham
College. He has been named by The
Independent on Sunday as one of the
UK
's leading scientists. In 2001 he won the prestigious Berwick
Prize of the London Mathematical Society, which is awarded every
two years to reward the best mathematical research by a
mathematician under forty.
In The
Story of Maths,
he
says Indians
made many of these breakthroughs before
Newton
was born.
The
Story of Maths, a four-part series, will be screened on BBC Four
in 2008. The first part looks at the development of maths in
ancient
Greece
, ancient
Egypt
and
Babylon
; the second focuses on
India,
China
and
Central Asia
and the rest look at how maths developed in the West. The India
reel focuses on how several Indians developed theories in maths
that were later discovered by Westerners
who took credit for them.
Aryabhatta
(476–550 AD), who calculated pi, and Brahmagupta
(598-670
AD) feature in the film, which also showcases a
Gwalior
temple, which documents the first inscription of 'zero'. "One
of the biggest inventions in
India
was the number zero. Indians used it long before the West
did," said Du Sautoy. "When the West had Roman numerals
there was no zero and that is why they were so clumsy. On the
other hand, Brahmagupta was one of the key mathematicians in the
world because he invented the idea of zero."
The
documentary also features the history of Kerala-born mathematician
Madhava (1350-1425) who created calculus 300 years before
Newton
and German mathematician Gottfried Leibniz did, said Du Sautoy.
"We
learn that
Newton
invented the mathematical theory calculus in the 17th
century but Madhava created it earlier,"
Du Sautoy said.
(source: Oxford
prof documents India's math contribution – By Naomi Canton,
Hindustan Times July 5, 2007).
Not
Newton, but Madhava!
Subsets of calculus existed in the Ganita-Yukti-Bhasa
two centuries before Isaac Newton published his work, according to
a recently published translation of the manuscript.
 Prof
K Ramasubramanian of IIT-Bombay has recently released
two-volume translation of the Ganita-Yukti-Bhasa
by Jyesthdeva points to the fact that
some subsets of calculus existed in Indian manuscripts almost two
centuries before Isaac Newton published his work. Prof
K Ramasubramanian of IIT-Bombay has recently released
two-volume translation of the Ganita-Yukti-Bhasa
by Jyesthdeva points to the fact that
some subsets of calculus existed in Indian manuscripts almost two
centuries before Isaac Newton published his work.
And that an Indian mathematician and astronomer Nilakantha
Somayaji spoke, in parts, about a planetary model,
credited to Tycho Brahe almost a century later.
In the Tantra
Sangraha (The Tantra Sangraha is a treatise on
astronomy and related mathematics in elegant verse form, in
Sanskrit. It consists of 432 verses.) Nilakantha
talks about a planetary model where five planets, which
can be seen with the naked eye – Mercury, Venus, Mars, Jupiter
and Saturn – move around the sun, which in turn moves around the
earth.
The
fact remains that a century later, Tycho
Brahe published the same planetary model and was credited for it,
since no one knew of Nilakantha’s work.
(source: Not
Newton, but Madhava! - mumbaimmirror.com).
 Dr
George Gheverghese Joseph from the
University
of
Manchester
and author of best-selling
book 'The Crest of the Peacock: the
Non-European Roots of Mathematics' said
the '
Kerala
School
' identified the 'infinite series 'one of the basic components of
calculus- -way back in AD1350. Dr
George Gheverghese Joseph from the
University
of
Manchester
and author of best-selling
book 'The Crest of the Peacock: the
Non-European Roots of Mathematics' said
the '
Kerala
School
' identified the 'infinite series 'one of the basic components of
calculus- -way back in AD1350.
"The
beginnings of modern maths is usually seen as a European
achievement, but the discoveries in medieval
India
between the 14th and 16th centuries have
been ignored or forgotten."
"The
brilliance of
Newton
's work at the end of the 17th century stands
undiminished - especially when it came to algorithms of calculus.
But other names from the Kerala School, notably Madhava
and Nilakantha,
should stand shoulder to shoulder with him as they discovered the
other great component of calculus- infinite series."
The
discovery is now attributed in math books to British scientist Sir
Isaac Newton and his German contemporary Gottfried Leibnitz at the
end of the 17th century. There was strong
circumstantial evidence that the Indians passed on their
discoveries to mathematically knowledgeable Jesuit
missionaries who visited
India
during the 15th century.
That
knowledge may have eventually been passed on to
Newton
himself, he said.
"It's
hard to imagine that the West would abandon a 500-year-old
tradition of importing knowledge and books from
India
and the Islamic world. But we've found evidence there was plenty
of opportunity to collect the information as European Jesuits were
present in the area at that time."
"They
were learned with a strong background in maths and were well
versed in the local languages. And there was strong motivation:
Pope Gregory XIII set up a committee to look into modernising the
Julian calendar. On the committee was the
German Jesuit astronomer/mathematician Clavius, who repeatedly
requested information on how people constructed calendars in other
parts of the world. The
Kerala
School
was undoubtedly a leading light in this area. "Similarly
there was a rising need for better navigational methods including
keeping accurate time on voyages of exploration and large prizes
were offered to mathematicians who specialised in astronomy.
"There
were many such requests for information across the world from
leading Jesuit researchers in
Europe
. Kerala mathematicians were hugely skilled in this area." There
were many reasons why the contribution of the
Kerala
School
has not been acknowledged till now. A prime reason, was the "neglect
of scientific ideas emanating from the Non-European world - a
legacy of European colonialism and beyond".
"But
there is also little knowledge of the medieval form of the local
language of Kerala, Malayalam, in which some of most seminal
texts, such as the Yuktibhasa, from much of the documentation of
this remarkable mathematics is written." "For some
unfathomable reasons, the standard of evidence required to claim
transmission of knowledge from East to West is greater than the
standard of evidence required to knowledge from West to East."
The
Kerala
School
also discovered what amounted to the Pi series and used it to
calculate Pi correct to 9, 10 and later 17 decimal places.
(source:
When
Kerala scholars beat
Newton
- rediff.com
and Indians
Predated Newton 'Discovery' By 250 Years, Scholars Say
- sciencedaily.com).
 Brian
Clegg ( ? ) author of popular science books has
written: Brian
Clegg ( ? ) author of popular science books has
written:
"The
characters we use for the numbers arrived here from India via the
Arabic world. The Brahmi numerals that have been found
in caves and on coins around Mumbai from around the first century
AD use horizontal lines for 1 to 3. The squiggles used for 4 to 9,
however, are clear ancestors of the numbers we use today. These
symbols were gradually taken up by Arabs and came to Western
attention in the 13th century thanks to two books, on
written by a traveler from Pisa, the other by a philosopher in
Baghdad. The earlier book was written by the philosopher al-Khwarizmi
in the 9th century. The Latin translation Algoritmi de
numero Indorum (al-Khwarizmi on the
numbers of the Hindus).
The
translation of De numero Indorum slightly predates the man who is
credited with introducing the system to the West. Leonardo of
Pisa, or by his nickname Fibonacci. In the comments in his book
Liberabaci, written in 1202, he states that he
was “introduced to the art of Indian’s nine symbols” and it
was this book that really brought the Hindu system to the West.
(source:
Infinity:
The Quest to Think the Unthinkable - By Brian Clegg
p. 54 - 60).
Carl
B. Boyer (1906 – 1976) in his "History
of Mathematics" pages 227-228”.
“...Mohammed ibn-Musa al-Khwarizmi, ..., who died sometime
before 850, wrote more than a half dozen astronomical and
mathematical works, of which the earliest were probably based on
the Sindhind derived from India.
Besides ... [he] wrote two books on arithmetic and algebra which
played very important roles in the history of mathematics. ... In
this work, based presumably on an Arabic translation of
Brahmagupta, al-Khwarizmi gave so full an account of the Hindu
numerals that he probably is responsible for the widespread but
false impression that our system of numeration is Arabic in
origin. ...
Edward Sachau, In a
translation of Alberuni
‘s “Indica”, a seminal work of this period
(c.1030 AD), writes this in his introduction, “Many
Arab authors took up the subjects communicated to them by the
Hindus and worked them out in original compositions , commentaries
and extracts. A favourite subject of theirs was Indian
mathematics..." etc.
“
Al-Khwarizmi wrote numerous books that played important roles in
arithematic and algebra. In his work, De numero indorum (Concerning
the Hindu Art of Reckoning),
it was based presumably on an Arabic translation of Brahmagupta
where he gave a full account of the Hindu numerals which was the
first to expound the system with its digits 0,1,2,3,....,9 and
decimal place value which was a fairly recent arrival from India.
Because of this book with the Latin translations made a false
inquiry that our system of numeration is arabic in origin. The new
notation came to be known as that of al-Khwarizmi, or more
carelessly, algorismi; ultimately the scheme of numeration making
use of the Hindu numerals came to be called simply algorism or
algorithm, a word that, originally derived from the name al-Khwarizmi,
now means, more generally, any peculiar rule of procedure or
operation.
Interestingly, as the article notes, “The
Hindu numerals like much new
mathematics were not welcomed by all. In 1299 there was a law in
the commercial center of Florence forbidding their use; to this
day this law is respected when we write the amount on a check in
longhand .”
“It
is now universally accepted that our decimal numbers derive from
forms, which were invented in India and transmitted via Arab
culture to Europe, undergoing a number of changes on
the way. We also know that several different ways of writing
numbers evolved in India before it became possible for existing
decimal numerals to be marred with the place-value principle of
the Babylonians to give birth to the system which eventually
became the one which we use today. Because of lack of authentic
records, very little is known of the development of ancient Hindu
mathematics. The earliest history is preserved in the
5000-year-old ruins of a city at Mohenjo Daro, located Northeast
of present-day Karachi in Pakistan. Evidence
of wide streets, brick dwellings an apartment houses with tiled
bathrooms, covered city drains, and community swimming pools
indicates a civilisation as advanced as that found anywhere else
in the ancient Orient.
These
early peoples had systems of writing, counting, weighing, and
measuring, and they dug canals for irrigation. All this required
basic mathematics and engineering. “The special
interest of the Indian system is that it is the earliest form of
the one, which we use today. Two and three were represented by
repetitions of the horizontal stroke for one. There
were distinct symbols for four to nine and also for ten and
multiples of ten up to ninety, and for hundred and thousand.”
“…Knowledge of the
Hindu system spread through the Arab world, reaching the Arabs of
the West in Spain before the end of the tenth century. The
earliest European manuscript, which came from the Hindu numerals
were modified in north-Spain from the year 976.” And finally an
important point for those who maintain that the concept of zero
was also evident in some other civilisations: “Only
the Hindus within the context of Indo-European civilisations have
consistently used zero.”
(source:
Hindu
contribution to Mathematics
- By B Shantanu - indiacause.com). Watch
Carl
Sagan and Hindu cosmology – video
 David
Mumford, the eminent mathematician writes in his review of the book, Mathematics
in India by Kim Plofker: David
Mumford, the eminent mathematician writes in his review of the book, Mathematics
in India by Kim Plofker:
"Did
you know that Vedic priests were using the so-called Pythagorean theorem to
construct their fire altars in 800 BCE?; that the differential equation for the
sine function, infinite difference form, was described by Indian
mathematician-astronomers in the fifth century CE?; and that 'Gregory's' series
PI/4 = 1 -1/3+1/3-… was proven using the power series for arctangent and, with
ingenious summation methods, used to accurately compute PI in southwest India in
the fourteenth century?
(source:
Mathematics
in India - Reviewed by David Mumford - AMS
American Mathematical Society - Volume 57
Number 3).
Gopala and Hemachandra and rhythmic patterns
 Donald
Knuth (1938 - ) of
Stanford University in The
Art of Computer Programming also wrote about this: Donald
Knuth (1938 - ) of
Stanford University in The
Art of Computer Programming also wrote about this:
"Before Fibonacci wrote his work, the sequence Fn had already
been discussed by Indian scholars, who had long been interested
in rhythmic patterns that are formed from one-beat and two-beat
notes. The number of such rhythms having n beats altogether is
Fn+1; therefore both Gopala
(before 1135) and Hemachandra
(c. 1150) mentioned the numbers 1, 2, 3, 5, 8, 13, 21, ...
explicitly."
The system that Fibonacci
introduced into Europe came from India and used the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9 with, most importantly,
a symbol for zero 0.
(source:
Who
was
Fibonacci?
and Origins
of Fibonacci number and Fibonacci
numbers or Hemecandra numbers? and
Gopala
and Hemachandra
numbers everywhere - sepiamutiny.com
Hemachandra).
Ian
G. Pearce ( ? ) has written: “Mathematics has long
been considered an invention of European scholars, as a result
of which the contributions of non-European countries have been
severely neglected in histories of mathematics. Worse
still, many key mathematical developments have been wrongly
attributed to scholars of European origin. This has led to
so-called Eurocentrism. ...The purpose of my project is to highlight the
major mathematical contributions of Indian scholars and further
to emphasize where neglect has occurred and hence elucidate why
the Eurocentric
ideal is an injustice and in some cases complete
fabrication.”
 “It is through the
works of Vedic religion that we gain the first literary evidence
of Indian culture and hence mathematics. Written in Vedic
Sanskrit the Vedic works, Vedas and Vedangas (and later
Sulbasutras) are primarily religious in content, but embody a
large amount of astronomical knowledge and hence a significant
knowledge of mathematics. ... 'The need to determine the correct
times for Vedic ceremonies and the accurate construction of
altars led to the development of astronomy and
geometry.'” “It is through the
works of Vedic religion that we gain the first literary evidence
of Indian culture and hence mathematics. Written in Vedic
Sanskrit the Vedic works, Vedas and Vedangas (and later
Sulbasutras) are primarily religious in content, but embody a
large amount of astronomical knowledge and hence a significant
knowledge of mathematics. ... 'The need to determine the correct
times for Vedic ceremonies and the accurate construction of
altars led to the development of astronomy and
geometry.'”
“I feel it important
not to be controversial or sweeping, but it is likely European
scholars are resistant due to the way in which the inclusion of
non-European, including Indian, contributions shakes
up views that have been held for hundreds of years, and
challenges the very foundations of the Eurocentric ideology. ...
It is almost more in the realms of psychology and
culture that we argue about the effect the discoveries of
non-European science may have had on the 'psyche' of European
scholars. ... To summarize, the main
reasons for the neglect of Indian mathematics seem to be
religious, cultural and psychological”
(source:
Indian
Mathematics: Redressing the balance' - 'Abstract' - By Ian
G. Pearce – '(IGP-IM:RB)
'Mathematics
in the service of religion: I. Vedas and Vedangas' and
Conclusion.
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju
Remarking
on this valuable contribution specially the discovery of number from one to nine
and zero, which is considered to be the greatest and the most important, next
only to the introduction of letters, Prof. Halsted of USA holds that no
discovery in Arithmetic has contributed so much in the development of human
intelligence and power. The Hindus can claim to be superior to the Greeks for
the introduction of this system.
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda Calcutta, Oxford
Book Co. 1962 p. 121).
Zero is the embodiment of purna
(full), lopa (absence), akasa (universe), bindu (dot), sunya
(circle), in Indian literary and cultural traditions. The
concept got concretized in the form of a symbol like dot or
circle to fill up the empty space created in Indian decimal
place-value concept. The scientific
advances of the West would have been impossible had scientists
continued to depend upon the Roman numerals and been deprived of
the simplicity and flexibility of the decimal system and its
main glory, the zero.
A 10th century traveler Masaudi, in his Arabic
work Meadows of Gold, records that a Hindu Raja called Pandit who counted nine
digits by memory. Abu Zafar Muhammad Al Khwarizm also mentions Hindu
mathematicians, as does Al Beruni. In the Journal of the Bengal Asiatic Society
(1907 p. 475), Feroz Abadi is quoted to have given the history of ‘Hindsa’
(= 0).
The number ‘10’ is a special contribution of
Hindu arithmetic. So the zero was called ‘Hindsa’ in Persian.
(source:
Hinduism: Its Contribution to Science and Civilization
- By Prabhakar Balvant Machwe p. 10-14).
Muhammad ibn Musa al-Khawarazmi 772-773 A.D. who
journeyed east to India to learn the sciences of that time. He introduced Hindu
numerals, including the concept of zero, into the Arab world. Abu Abdulla
Muhammad Ibrahim-al-Fazari translated Sidhanta
from Sanskrit into Arabic, which, according to George
Sarton (1884-1956)
the great Harvard historian of science, wrote in his monumental Introduction
to the History of Science, provided
"possibly the vehicle by means of which the Hindu numerals were transmitted
from India to Islam".
***
Algebra
Brahmagupta gives the
following rules concerning operations carried out on what he calls
“fortunes” (dhana), “debts” (rina) and “nothing” (kha).
A debt minus zero is a debt.
A fortune minus zero is a fortune.
Zero (shunya) minus zero is nothing. (kha).
A debt subtracted from zero is a fortune.
So a fortune subtracted from zero is a debt.
The product of zero multiplied by a debt or fortune is zero.
The product of zero multiplied by itself is nothing.
The product or the quotient of two fortunes is one fortune.
The product or the quotient of two debts is one debt.
The product or the quotient of a debt multiplied by a fortune is a
debt.
The product or the quotient of a fortune multiplied by a debt is a
debt.
Modern algebra was born, and the
mathematician had thus formulated the basic rules: by replacing
“fortune” and “debt” respectively with “positive
number” and “negative number”, we can see that at that time
the Indian mathematicians knew the famous “rule of signs” as
well as all the fundamental rules of algebra.
(source:
The
Universal History of Numbers - By Georges
Ifrah p 439).
 Florian
Cajori (1859 - 1930) Swiss-born U.S. educator and mathematician whose works
on the history of mathematics says: Florian
Cajori (1859 - 1930) Swiss-born U.S. educator and mathematician whose works
on the history of mathematics says:
"Indians were the “real inventors of Algebra”
(source:
Is
India Civilized - Essays on Indian Culture - By Sir John
Woodroffe Ganesh & Co. Publishers 1922 p. 182).
Friedrich Rosen
(1805-1837) edited and translated in 1831, The
Algebra of Mohammed ben Musa. This is the oldest Arabic on mathematics and it
shows that the Arabs borrowed algebra from India.
(source: German
Indologists: Biographies of Scholars in Indian Studies writing in German
- By Valentine Stache-Rosen p.24-25).
Algebra went to
Western Europe from the Arabs - i.e. (Al-jabr, adjustment) who adopted it from
India rather than from Greece. Sir Monier-Williams, T. S. Colebrooke, and
Macdonell hold that the Arabs got Algebra from the Hindus. The great Indian leaders in this field, as in
astronomy were
Aryabhata, Brahmagupta, and Bhaskara.
The last appears to have invented
the radical sign and many algebraic symbols. These men created the conception of
a negative quantity, without which algebra would have been impossible; they
found the square root of 2, and solved, in the eighth century A.D.,
indeterminate equations of the second degree that were
unknown
to Europe until the days of Euler a thousand years later. They
expressed their science in poetic form and gave to mathematical problems a grace
characteristic to India's Golden Age.
Henry Thomas Colebrooke (1765-1837)
wrote: "They (the Hindus) understood well the arithmetic of surd roots;
they were aware of the infinite quotient resulting from the division of finite
quantities by cipher; they knew the general resolution of equations of the
second degree, and had touched upon those of higher denomination, resolving them
in the simplest cases, and in those in which the solution happens to be
practicable by the method which serves for quadratics; they had attained a
general solution of indeterminate problems of the first degree; they had arrived
at a method for deriving a multitude of solutions or answers to problems of the
second degree from a single answer found tentatively."
"And this, says Colebrooke in conclusion,
was as near an approach to a general solution of such problems as was made until
the days of La Grange."
(source:
Miscellaneous
Essays - By H. T. Colebrooke Volume II p. 416 - 418).

" Out of a swarm of bees one-fifth
part settled on a Kadamba blossom; one-third on a Silindhra flower; three times
the difference of those numbers flew to the bloom of a Kutaja. One bee, which
remained, hovered about in the air. Tell me, charming woman, the number of bees
...Eight rubies, ten emeralds, and a hundred pearls, which are in thy ear-ring,
my beloved, were purchased by me for thee at an equal amount; and the sum of the
prices of the three sorts of gem was three less than half a hundred; tell me the
price of each, auspicious woman."
***
"The
Indian mind has always had for calculations and the handling of
numbers an extraordinary inclination, ease and power, such as no
other civilization in history ever possessed to the same degree.
So much so that Indian culture regarded the science of numbers
as the noblest of its arts."
Refer
to Indian
Institute of Scientific Heritage
  
Aryabhata
(475 A.D. - 550 A.D.) is the first well known Indian mathematician. Born in
Kerala, he completed his studies at the university of Nalanda. In the section Ganita
(calculations) of his astronomical treatise Aryabhatiya
(499 A.D.) he made the fundamental
advance in finding the lengths of chords of circles, by using the half chord
rather than the full chord method used by Greeks. He gave the value of pi as
3.1416, claiming, for the first time, that it was an approximation. (He gave it
in the form that the approximate circumference of a circle of diameter 20000 is
62832.) He also gave methods for extracting square roots, summing arithmetic
series, solving indeterminate equations of the type ax - by = c, and also
gave what later came to be known as the table of Sines. He also wrote a text
book for astronomical calculations, Aryabhatasiddhanta. Even today, this
data is used in preparing Hindu calendars (Panchangs). In recognition to
his contributions to astronomy and mathematics, India's first satellite was
named Aryabhata.

Aryabhatta
(475 A.D. - 550 A.D).
Aryabhatta put forward a brilliant thesis with regard to
the Earth's rotation on its axis.
(image source: Vishwa
Hindu Parishad of America. Inc - 2002 calendar).
***
 Soviet historians, K.
Antonova, G. Bongard-Levin, and G. Kotovsky, authors of A
History of India, Moscow, Volume I and II 1973, have spoken
highly of scientists of ancient India and their high originality: Soviet historians, K.
Antonova, G. Bongard-Levin, and G. Kotovsky, authors of A
History of India, Moscow, Volume I and II 1973, have spoken
highly of scientists of ancient India and their high originality:
"In the ancient period and in the early
Middle Ages lived the outstanding mathematicians Aryabhatta
(5-6th centuries), Varahamihira (6th
century) and Brahmagupta (late 6th and early
7th centuries), whose discoveries anticipated many scientific achievements of
modern times. Aryabhata knew that pi equaled 3.1416. The theorem known to us as
Pythagoras' theorem was also known at that time. Aryabhata proposed an original
solution in whole numbers to the linear equations with two unknowns that closely
resembles modern solutions.
"The ancient Indians evolved a system for
calculation using zero, which was later taken over by the Arabs (the so-called
Arabic numerals) and alter from them by other peoples. The Aryabhatta school was
also familiar with sine and cosine.
"Scholars of the Gupta period were already
acquainted with the movement of the heavenly bodies, the reasons for eclipses of
the Sun and the Moon. Aryabhatta put forward a brilliant thesis with regard to
the Earth's rotation on its axis."
"Aryabhatta's follower, Brahmagupta, put
forward solutions for a whole series of equations."
"Indian scholars of this period also scored
important successes in the sphere of astronomy. Certain astronomical treatises
of this period have been preserved, and these siddhantas bear witness to the
high level of astronomical knowledge attained by the ancient Indians."
"Brahmagupta (many
centuries before Newton) suggested that objects fall to the ground as a result
of terrestrial gravity."
"Interesting material relating to astronomy,
geography and mineralogy is found in Varahamihira's work Brihat-samhita...."
(source: A
History of India - By K. Antonova, G.
Bongard-Levin, and G. Kotovsky
Moscow, Volume I and II 1973 p. 169-171).
Aryabhatta was a great astronomer of remarkable
originality. He is famous for his suggestions of the diurnal revolution of the
earth on its own axis. Another important conclusion was about the apparent
motion of the sun and the moon. He observes: "The
starry vault is fixed: it is the earth which, moving on its own axis, seems to
cause the rising and the setting of the planets and stars."
(source: Main Currents
in Indian Culture - By S. Natarajan - The Institute of Indo-Middle
East Cultural Studies. 1960. p 62-63).
Yavadvipa,
the ancient name for Java, to which Sugriva sent search parties looking for Sita,
is a Sanskrit name mentioned in the Ramayana. Aryabhatta wrote that when the sun
rose in Sri Lanka, it was midday in Yavakoti (Java) and midnight in the Roman
land. In the Surya Siddanata reference is also made to the Nagari Yavakoti with
golden walls and gates.
(source:
India and World Civilization
- By D. P. Singhal Pan Macmillan Limited. 1993.
p. 323).
Mnemonic and shorthand code letters were used by the Hindu
astronomer Aryabhat, who composed his
Aryabhatiya in 499 A.D. He answers the question: “How many times does the
Earth rotate in a Mahayuga?” by the sutra – Ngishi Bunlrukshshru. Its
letters count up to 15,82,23,75,200.
The second Aryabhatta (II)
has also given such cryptic numberal-alphabets:
Kanadhajhajhujhila =
1599993
Mudayasinadha =
58179
(source:
Hinduism: Its Contribution to Science and Civilization
- By Prabhakar Balvant Machwe p. 10-14).
Comparing the Hindus and the Greeks as regards
their knowledge of algebra, Sir Mountstuart Elphinstone
says:
"There is no question of the
superiority of the Hindus over their rivals in the perfection to which they
brought the science. Not only is Aryabhatta superior to
Diaphantus (as is shown by his knowledge of the resolution of
equations involving several unknown quantities, and in general method of
resolving all indeterminate problems of at least the first degree), but he and
his successors press hard upon the discoveries of algebraists who lived almost
in our own time!"
(source: History
of India - By Mountstuart Elphinstone London: John Murray Date of
Publication: 1849 p. 131).
 The Aryabhatiya
was translated into Latin in the 13th century. Through this
translation European mathematicians eventually learned methods for calculating
the squares of triangles and the volumes of spheres, as well as square and cube
roots. He had conceptualized the ideas about the cause
of eclipses and the sun being the source of moonlight a thousand years before
the Europeans. A revolutionary
thinker in many areas, Aryabhata gave the radius of the planetary orbits in
terms of the radius of the earth-sun orbit – that is, their orbits as
basically their periods of rotation around the sun. He explained that the glow
of the moon and planets was the result of reflected sunlight. And
with incredible astuteness, he conceptualized the orbits of the planets as
ellipses, a thousand years before Kepler reluctantly (he originally preferred
circles) came to the same conclusion. His value for the length of the
year at 365 days, six hours, twelve minutes, and thirty seconds, however, is a
slightly overestimate; the true value is fewer than 365 days and 6 hours. The Aryabhatiya
was translated into Latin in the 13th century. Through this
translation European mathematicians eventually learned methods for calculating
the squares of triangles and the volumes of spheres, as well as square and cube
roots. He had conceptualized the ideas about the cause
of eclipses and the sun being the source of moonlight a thousand years before
the Europeans. A revolutionary
thinker in many areas, Aryabhata gave the radius of the planetary orbits in
terms of the radius of the earth-sun orbit – that is, their orbits as
basically their periods of rotation around the sun. He explained that the glow
of the moon and planets was the result of reflected sunlight. And
with incredible astuteness, he conceptualized the orbits of the planets as
ellipses, a thousand years before Kepler reluctantly (he originally preferred
circles) came to the same conclusion. His value for the length of the
year at 365 days, six hours, twelve minutes, and thirty seconds, however, is a
slightly overestimate; the true value is fewer than 365 days and 6 hours.
"Brahmagupta became the head of
the astronomical observatory at Ujjain, the foremost mathematical center of
ancient India, where great mathematicians such as Varahamihira
had worked and built a strong school of mathematical astronomy.
The Brahmasphutasidhanta
contains 25 chapters, the first ten of which are arranged by topics such as true
longitudes of the planets, lunar eclipses, solar eclipses, rising and settings,
the moon’s crescent, the moon’s shadow, conjunctions of the planets with the
fixed stars. A large part of the Brahmasphutsidhanta was translated into Arabic
in the early 770s and became the basis of various studies by the astronomer
Ya’qub ibn Tariq. In 1126 it was translated into Latin. This translation,
along with other associated texts translated from Arabic, provided the basis for
the Indo-Arabic stage of Western astronomy. The
culmination of southern Indian astronomy was the tradition begun by Madhava in
Kerala right before 1400. Madhava was
renowned for his derivation of the infinite series for pi and the power series
for trigonometric functions. His pupil Paramesvara
attempted to correct the lunar parameters by conducting a long series of eclipse
observations between 1393 and 1432. In these observations he used an astrolabe,
an instrument devised to measure the positions of heavenly bodies, to determine
the angle of altitude of the eclipsed body and possibly, the time of the phase
of the eclipses."
(source:
Lost
Discoveries: The Ancient Roots of Modern Science - By Dick
Teresi p. 133 - 136).
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju
In the Jewish
Encyclopedia Vol. XII p 689, it is noted,
"Aryabhatta, the noted Hindu astronomer who
lived about 476 A.D. and who is called the Newton of the country, wrote many
works on Algebra and Geometry. He first discovered the rotation of the earth
round its own axis. As a Jewish writer says the theory that earth is a sphere
revolving round its own axis which immortalized Copernicus, was previously known
to the Hindus, who were instructed in the truth of it by Aryabhatta."
Jogesh Chandar Roy
(1859-1965) Eminent scholar, educationist,
writer, linguist, historian. Owing to his talent was conferred many accolades
like D.Litt., Acharya, Bidyanidhi, Roy Bahadur etc. He held that the Vedic sages
first admitted that the world is round ohterwise the advent of dawn (Usha) in
the hymns, before sunrise becomes meaningless."
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda
Calcutta, Oxford Book Co. 1962
p. 126).
Arya
Bhatta (476 - 550 AD) Father of Astronomy, who in the fifth century AD that is over a
millennium and a half ago very accurately calculated many aspects of the
spinning earth.
Arya Bhatta"s seminal work Aryabhatiyam was translated in to Arabic in the ninth century and subsequently it
journeyed further west. Four hundred years later in the thirteenth century this
treatise on astronomy was translated into Latin. The Latin version of
Aryabhatiyam provided the foundation for growth of astronomy in
Europe
. I want my readers to appreciate that the Hindu astronomers of
India
built the foundation for European astronomy to stand and flourish. Arya Bhatta
in a chapter of his treatise entitled Gola,
which means circle or sphere, very categorically demonstrates the sphericity of
earth, way before any European astronomer even had the vaguest inkling as to the
size and shape of our planet. Arya Bhatta"s calculation of the equatorial circumference of earth at
39,968 km is only marginally less (by 62 km) of 40,076 km that we accept today.
His calculated duration of one complete rotation of earth round its axis, which
in common parlance is stated as 1 day, is absolutely correct at 23 hours 56
minutes and 4.1 seconds. Arya
Bhatta also calculated the value of Pi with remarkable accuracy, and laid the
foundation of many disciplines of mathematics that included trigonometry and
mensuration.
(source:
- indiacause.com).
 
 Brahmagupta
(598 A.D. - 665 A.D.) is renowned for introduction of negative numbers and
operations on zero into arithmetic. His main work was Brahmasphutasiddhanta,
which was a corrected version of old astronomical treatise Brahmasiddhanta.
This work was later translated into Arabic as Sind
Hind. He formulated the rule of three and proposed
rules for the solution of quadratic and simultaneous equations. He was the first mathematician to treat algebra and
arithmetic as two different branches of mathematics. He gave the solution of the
indeterminate equation Nx2+1 = y2. He is also the founder
of the branch of higher mathematics known as "Numerical Analysis". Brahmagupta
(598 A.D. - 665 A.D.) is renowned for introduction of negative numbers and
operations on zero into arithmetic. His main work was Brahmasphutasiddhanta,
which was a corrected version of old astronomical treatise Brahmasiddhanta.
This work was later translated into Arabic as Sind
Hind. He formulated the rule of three and proposed
rules for the solution of quadratic and simultaneous equations. He was the first mathematician to treat algebra and
arithmetic as two different branches of mathematics. He gave the solution of the
indeterminate equation Nx2+1 = y2. He is also the founder
of the branch of higher mathematics known as "Numerical Analysis".
The
Hindus were aware of the length of diameter and circumference of the earth.
According to Brahmagupta and Bhaskarachary the diameter is 7182 miles, some
calculate it to be 7905 miles, modern scientists take it to be 7918 miles. For
the sake of astronomical experiments the Hindus introduced Sanka Yantra and
Ghati Yantra, the apparatus for measurement.
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda
Calcutta, Oxford Book Co. 1962 p. 126).
After Brahmagupta, the mathematician of some
consequence was Sridhara, who wrote Patiganita
Sara, a book on algebra, in 750 A.D. Even Bhaskara refers to his works.
After Sridhara, the most celebrated mathematician was Mahaviracharaya
or Mahavira. He wrote Ganita Sara Sangraha in 850 A.D., which
is the first text book on arithmetic in present day form. He is the only Indian
mathematician who has briefly referred to the ellipse (which he called Ayatvrit).
The Greeks, by contrast, had studied conic sections in great detail.
Bhaskara
(1114 A.D. - 1185 A.D.) or Bhaskaracharaya
is the most well known ancient Indian mathematician. He was born in 1114 A.D. at
Bijjada Bida (Bijapur, Karnataka) in the Sahyadari Hills. He
was the first to declare that any number divided by zero is infinity and that
the sum of any number and infinity is also infinity. He is famous for his
book Siddhanta Siromani (1150 A.D.). It is divided into four sections - Leelavati
(a book on arithmetic), Bijaganita (algebra), Goladhayaya (chapter
on sphere - celestial globe), and Grahaganita
(mathematics of the planets). Leelavati contains many interesting
problems and was a very popular text book. Bhaskara introduced chakrawal,
or the cyclic method, to solve algebraic equations. Six
centuries later, European mathematicians like Galois, Euler and Lagrange
rediscovered this method and called it "inverse cyclic".
Bhaskara can also be called the founder of differential calculus. He gave an
example of what is now called "differential coefficient" and the basic
idea of what is now called "Rolle's theorem". Unfortunately, later
Indian mathematicians did not take any notice of this. Five centuries later,
Newton and Leibniz developed this subject. As an astronomer, Bhaskara is
renowned for his concept of Tatkalikagati (instantaneous motion).
(source: Ancient
Indian Mathematicians and http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Bhaskara_II.html).
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju
 “A Persian translation of the
Veeju-Ganitu was made in India,” says Mr. Edward Strachey, “in the year
1634, by Ata Oollah Rusidee.” The same gentlemen says, “Foizee, in 1587,
translated the Leelavatee, a work on arithmetic, mensuration,” etc. from which
work it appears that “Bhaskara must have
written about the end of the 12th century..” “A Persian translation of the
Veeju-Ganitu was made in India,” says Mr. Edward Strachey, “in the year
1634, by Ata Oollah Rusidee.” The same gentlemen says, “Foizee, in 1587,
translated the Leelavatee, a work on arithmetic, mensuration,” etc. from which
work it appears that “Bhaskara must have
written about the end of the 12th century..”
“We must not,” adds Edward
Strachey author of Bija
ganita; or, The algebra of the Hindus, “be too fastidious in our
belief, because we have not found the works of the teachers of Pythagoras; we
have access to the wreck only of their ancient learning; but when such traces of
a more perfect state of knowledge; we see that the Hindoo algebra 600 years ago, had, in the most
interesting parts, some of the most curious modern European discoveries, and
when we see, that it was at that time applied to astronomy, we cannot reasonably
doubt the originality and the antiquity of mathematical learning among the
Hindoos.”
(source: A
View of the History, Literature, and Mythology of the Hindoos -
By William Ward (1769-1823)
volume II p 329 London
1822).
Sir Mountstuart
Elphinstone wrote: "In the Surya Siddhanta is contained a system
of trigonometry which not only goes beyond anything known to the Greeks, but
involves theorem which were not discovered in Europe till two centuries
ago."
(source: Sanskrit
Civilization - By G. R. Josyer p. 2).
The discovery of the law of gravitation which
immortalized Newton was known in India by Bhaskaracharya
long before the birth of Newton. In support of the assumption of this view there
is sufficient evidence in a verse in Sidhanta Siromany
by its author. Bhaskaracharya holds that when the earth which is endowed with
the power of attraction drags with her own power heavy objects on the sky it
appears that objects are falling but actually they are not falling, they are
only being dragged by the power of attraction of the earth. When everything on
the sky drags each other equally where will the earth fall: It is explained that
earth, planets, stars, moon, sun etc - each of them is being dragged by the
other with its respective power of attraction and as a result of this attraction
none of them is removed from its axis.
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda
Calcutta, Oxford Book Co. 1962
p. 127).
Sir
William Wilson
Hunter
wrote:
"The Hindus attained a very high proficiency in arithmetic and algebra
independently of any foreign influence." The romance of the composition of Lilavati
- the standard Hindu text book on Arithmetic by Bhaskaracharya - is
very interesting and charming. It deals not only with the basic elements of the
science of arithmetic but also with questions of interest, of barter, of
permutations and combinations, and of mensuration. Bhaskaracharya knew the law
of gravitation. The Surya Siddhanta is based
on a system of trigonometry. Professor Wallace says: "In fact it is founded
on a geometrical theorem, which was not known to the geometricians of Europe
before the time of Vieta, about two hundred years ago. And it employs the sine
of arcs, a thing unknown to the Greeks." The 47th proposition of Book I of
Euclid, which is ascribed to Pythagoras was known long ago to the Hindus and
must have been learnt from them by Pythagoras.
(source: Indian Culture
and the Modern Age - By Dewan Bahadur K. S. Ramaswami Sastri
Annamalai University. 1956 p. 67).
For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
***
Geometry
Geometry, like Astronomy, owes its
origin in India to religion, and Grammar and Philosophy too were similarly
inspired by religion.
As George
Frederick William Thibaut (1848-1914) author of Mathematics
in the making in Ancient India, remarked: "The want of some rule
by which to fix the right time for the religious altar gave the first impulse to
astronomical observations; urged by this the priest, remained watching night
after night the advancement of the moon through the circle of the Nakshatras...The
laws of phonetics were investigated....the wrong pronunciation of a single
letter of the text; grammar and etymology had the task of securing the right
understanding of the holy texts. And Thibaut then lays down the principle, which
should never be overlooked by Indian historians, that
whatever science "is closely connected with the Ancient Indian religion,
must be considered as having sprung up among the Indians themselves, and not
borrowed from other nations."
Geometry was developed in India from
the rules of the construction of the altars. The Black Yajur Veda (V.4.11)
enumerates the different shapes in which altars could be constructed and
Baudhayana and Apastamba furnish us with full particulars about the shape of
these chitis and the bricks which had to be employed for their construction. The
Sulva Sutras date from the eighth century before Christ. The geometrical theorem
that the square of the hypotenuse is equal to the squares of the other two sides
of a rectangular triangle is ascribed by the Greeks to Pythagoras; but
it was known in India at least two centuries before, and Pythagoras undoubtedly
learnt this rule from India.
(source: Journal
of the Asiatic Society of Bengal, 1875. p. 227 and A
History of Civilization in Ancient India Based on Sanscrit
Literature - By Romesh Chunder Dutt p.
240-243)
 Vedic altars and sacrificial places were constructed
according to strict geometrical principles. The
Vedic (altar) had to be stacked in a geometrical form with the sides in fixed
proportions, and brick altars had to combine fixed dimensions with a fixed
number of bricks. Again, the surface areas were so designed that altars could be
increased in size without change of shape, which required considerable
geometrical ingenuity. Vedic altars and sacrificial places were constructed
according to strict geometrical principles. The
Vedic (altar) had to be stacked in a geometrical form with the sides in fixed
proportions, and brick altars had to combine fixed dimensions with a fixed
number of bricks. Again, the surface areas were so designed that altars could be
increased in size without change of shape, which required considerable
geometrical ingenuity.
Geometrical rules found in the Sulvasutras,
therefore, refers to the construction of squares and rectangles, the relation of
the diagonal to the sides, equivalent rectangles and squares, equivalent circles
and squares, conversion, of oblongs into squares and vice versa, and the
construction of squares equal to the sum or difference of two squares. In such
relations a prior knowledge of the Pythagorean theorem, that the square of the
hypotenuse of a right-angled triangle is equal to the sum of squares of the
other two sides, is disclosed.
In measurement and construction of altars the
priests formulated the Pythagorean theorem (by which the square of the
hypotenuse of a right-angled triangle equals the sum of the squares of the other
side) several hundred years before the birth of Christ.
As every schoolchild knows, the most important theorem
in geometry is that of Pythagoras. Yet, there is no evidence that either the
statement or the proof was known by the man to whom it is credited. The earliest
statement can be found in the Sulbasutra of Baudhyana. Baudhayana has preserved
its germination in religious rituals. The fact that ancient Indians knew this
theorem was recognized quite early by some European scholars. Among the first
was G. Thibaut,
a historian of science, who left the impression that in geometry the
Pythagoreans were the pupils of the Indians. Scholars unhappy with this idea
tried to refute it, thought their refutation was, as Abraham Seidenberg, noted,
were no more haughty dismissals.
The Formula known today as the Pythagorean
Theorem was first postulated by Indian mathematician -
Baudhayana in the 6th century C. E. long before Europe's math whizzies. In 497
C.E.
Aryabhatta calculated the value of
"pi" as 3.1416. Algebra, trigonometry and the concepts of algorithm, square root
originated in India. Quadratic equations were propounded by Sridharacharya in the 11th
century.
The largest number used by Greeks and Romans were 106, whereas Indians used numbers as
big as 10 to the power of 53, as early as 5000 BCE. Even geometry called
Rekha Ganita in
ancient India, was
applied to draft mandalas for architectural purposes and for creating temple motifs.
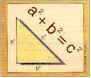 Professor
H. G. Rawlinson writes: " It is more likely that Pythagoras was
influenced by India than by Egypt. Almost all the theories, religions,
philosophical and mathematical taught by the Pythagoreans, were known in India
in the sixth century B.C., and the Pythagoreans, like the Jains and the
Buddhists, refrained from the destruction of life and eating meat and regarded
certain vegetables such as beans as taboo" "It seems that the
so-called Pythagorean theorem of the quadrature of the hypotenuse was already
known to the Indians in the older Vedic times, and thus before Pythagoras Professor
H. G. Rawlinson writes: " It is more likely that Pythagoras was
influenced by India than by Egypt. Almost all the theories, religions,
philosophical and mathematical taught by the Pythagoreans, were known in India
in the sixth century B.C., and the Pythagoreans, like the Jains and the
Buddhists, refrained from the destruction of life and eating meat and regarded
certain vegetables such as beans as taboo" "It seems that the
so-called Pythagorean theorem of the quadrature of the hypotenuse was already
known to the Indians in the older Vedic times, and thus before Pythagoras
(source: Legacy
of India 1937, p. 5).
Romesh
Chunder Dutt, the famous Indian historian holds that the world is
indebted to the Hindus for Geometry and not to the Greeks.
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda
Calcutta, Oxford Book Co. 1962
p. 124).
Professor
Maurice Winternitz is of the same opinion: "As regards
Pythagoras, it seems to me very probable that he became acquainted with Indian
doctrines in Persia." (Visvabharati Quarterly Feb. 1937, p. 8).
It is also the view of Sir
William Jones (Works, iii. 236), Colebrooke
(Miscellaneous Essays, i. 436 ff.). Schroeder (Pythagoras
und die Inder), Garbe (Philosophy
of Ancient India, pp. 39 ff), Hopkins
(Religions of India, p. 559 and 560) and
Macdonell (Sanskrit Literature,
p. 422).
(source: Eastern
Religions & Western Thought - By S. Radhakrishnan
ISBN: 0195624564
p. 143).
Ludwig
von Schröder German philosopher, author of the
book Pythagoras
und die Inder (Pythagoras and the Indians), published in 1884, he
argued that Pythagoras had been influenced by the Samkhya school of thought, the
most prominent branch of the Indic philosophy next to Vedanta.
(source:
In
Search of The Cradle of Civilization: : New Light on Ancient India - By
Georg Feuerstein, Subhash Kak & David Frawley
p. 252).
" Nearly all the philosophical and mathematical
doctrines attributed to Pythagoras are derived from India."
 Sir
William Temple, (1628-1699) English
statesman and diplomat, in his Essay upon the Ancient
and Modern Learning (1690) he wrote: Sir
William Temple, (1628-1699) English
statesman and diplomat, in his Essay upon the Ancient
and Modern Learning (1690) he wrote:
"From these famous Indians, it seems most
probable that Pythagoras learned, and transported into Greece and Italy, the
greatest part of his natural and moral philosophy, rather than from the
Aegyptians...Nor does it seem unlikely that the Aegyptians themselves might have
drawn much of their learning from the Indians..long before..Lycurgus, who
likewise traveled to India, brought from thence also the chief principles of his
laws."
Temple's ideas remained in isolation in his
period until they were revived in the middle of the 18th century when a battle
raged between the 'believers' and the 'infidels' on the question of the value of
Mosaic interpretation of history.
(source: Much
Maligned Monsters: A History of European Reactions to Indian Art - By Partha
Mitter p. 191).
Aryabhata,
found the area of a triangle, a trapezium and a circle, and
calculated the value of "pi" ( the relation of diameter to
circumference in a circle) at 3.1416 - a figure not equaled in accuracy until
the days of Purbach (1423-61) in Europe.
Bhaskara
anticipated the differential
calculus, Aryabhata drew up a table of sines, and the
Surya Siddhanta provided a
system of trigonometry more advance than anything known to the Greeks. He
had tabulated the sine function (unknown in Greece) for every 33/4º
of arc from 33/4º to 90º. By
670 the system had reached northern Mesopotamia,
where the Nestorian
bishop Severus Sebokht
praised its Hindu inventors as discoverers of things more ingenious than those
of the Greeks. Muslims
began the acquisition of foreign learning, and, by the time of the
Caliph al-Mansur
(d. 775),
such Indian and Persian astronomical material as the
Brahma-sphuta-siddhanta
and the Shah's Tables
had been translated into Arabic.
A
3,000-year-old ritual was resurrected at Panjal in Kerala in April 1975. A
12-day Agnicayana, or Atiratra, was performed on a bird-shaped altar of a
thousand bricks. The altar was a geometricians' delight.
The
area of each layer of the altar, for instance, was seven and a half times a
square purusa, the size of the sacrificer or the Yajamana. A fifth of the size
of the Yajamana, panchami, was the basic unit of the bricks.
 The
rules for measurement and construction of sacrificial altars are found in the
Sulba Sutras, the earliest documents of geometry in India. Sulba means cord. Of
the various Sulba Sutras, those of Baudhayana, Apastamba and Katyayana are best
known. The mathematical knowledge in the texts comes from the creation of altars
or bricks in various shapes-rhombus, isosceles trapezium, square, rectangle,
isosceles right-angled triangle or circle. A square-shaped altar sometimes had
to become circular without any change in the area or vice-versa. Obviously, the
authors of the Sulba texts knew the value of pi, which is the ratio of the
circumference to the diameter of a circle. The
rules for measurement and construction of sacrificial altars are found in the
Sulba Sutras, the earliest documents of geometry in India. Sulba means cord. Of
the various Sulba Sutras, those of Baudhayana, Apastamba and Katyayana are best
known. The mathematical knowledge in the texts comes from the creation of altars
or bricks in various shapes-rhombus, isosceles trapezium, square, rectangle,
isosceles right-angled triangle or circle. A square-shaped altar sometimes had
to become circular without any change in the area or vice-versa. Obviously, the
authors of the Sulba texts knew the value of pi, which is the ratio of the
circumference to the diameter of a circle.
The theory of right angles is attributed to Greek philosopher Pythagoras (6th
century BC). But Baudhayana mentions that the diagonal of a rectangle produces
by itself both (the areas) produced separately by its two sides. In simple
terms, this means that the square of the diagonal is equal to the sum of the
squares of two sides. In the next rule he says that the rectangles for which the
theorem is true have the sides as 3 and 4 [32+42=52], 12 and 5, 15 and 8, 7 and
24, 12 and 35, 15 and 36. The theorem is given in all the Sulba
Sutras.
Eminent
mathematician A. K. Bag, he says tackling of mathematical and geometrical
problems with rational numbers and irrational numbers [such as square-root of 2]
was a unique achievement of early Indians. They even had technical terms such as
dvikarani, trikarani and panchakarani (for square-roots of 2, 3 and 5) and so on
and gave their values to a high degree of approximation.
The mathematics in Sulba texts also involves a highly sophisticated brick
technology. Ten types of bricks were used to build the altar at
Panjal.
Sir
Monier-Williams says:
"To the Hindus is due the invention of algebra and geometry, and their
application to astronomy."
(source: Indian Wisdom -
By Monier Williams p. 185).
Count Magnus
Fredrik Ferdinand Bjornstjerna
author of Theogony
of the Hindus says: "We find
in Ayeen-Akbari, a journal of the Emperor Akbar, that the Hindus of former times
assumed the diameter of a circle to be to its periphery as 1,250 to 3,927. The
ratio of 1,250 to 3,927 is a very close approximation to the quandrature of a
circle, and differs very little form that given by Metius of 113 to 355. In
order to obtain the result thus found by the Brahmans, even in the most
elementary and simplest way, it is necessary to inscribe in a circle a poligon
of 768 sides, an operation, which cannot be performed arithmetically without the
knowledge of some peculiar properties of this curved line, and at least an
extraction of the square root of the ninth power, each to ten places of
decimals. The Greeks and Arabs have not given anything
so approximate."
Professor Wallace
says: "However ancient a book may be in which a system of trigonometry
occurs, we may be assured it was not written in the
infancy of the science. Geometry must have been known in India long before the
writing of Surya Siddanata." which is supposed by the Europeans
to have been written before 2000 B. C. E.
(source: Sanskrit
Civilization - By G. R. Josyer p. 2-3).
Influence of Hindu Geometry on Greeks:
 In his monumental work, The origin of
mathematics, Archive for History of Exact Sciences.
vol. 18, 301-342, Abraham Seidenberg
remarks:
"By
examining the evidence in the Shatapatha
Brahmana, we now know that Indian
geometry predates Greek geometry by centuries. For example, the earth was
represented by a circular altar and the heavens were represented by a square
altar and the ritual consisted of converting the circle into a square of an
identical area. There we see the beginnings of geometry! Two aspects of the 'Pythagoras' theorem are described
in the Vedic literature. One aspect is purely algebraic that presents numbers
a, b, c for which the sum of the squares of the first two equals the square of
the third. The second is the geometric, according to which the sum of the
areas of two square areas of different size is equal to another square. The
Babylonians knew the algebraic aspect of this theorem as early as 1700 BCE,
but they did not seem to know the geometric aspect. The Shatapatha Brahmana,
which precedes the age of Pythagoras, knows both aspects. Therefore, the
Indians could not have learnt it from the Old-Babylonians or the Greeks, who
claim to have rediscovered the result only with Pythagoras. India is thus the
cradle of the knowledge of geometry and mathematics." In his monumental work, The origin of
mathematics, Archive for History of Exact Sciences.
vol. 18, 301-342, Abraham Seidenberg
remarks:
"By
examining the evidence in the Shatapatha
Brahmana, we now know that Indian
geometry predates Greek geometry by centuries. For example, the earth was
represented by a circular altar and the heavens were represented by a square
altar and the ritual consisted of converting the circle into a square of an
identical area. There we see the beginnings of geometry! Two aspects of the 'Pythagoras' theorem are described
in the Vedic literature. One aspect is purely algebraic that presents numbers
a, b, c for which the sum of the squares of the first two equals the square of
the third. The second is the geometric, according to which the sum of the
areas of two square areas of different size is equal to another square. The
Babylonians knew the algebraic aspect of this theorem as early as 1700 BCE,
but they did not seem to know the geometric aspect. The Shatapatha Brahmana,
which precedes the age of Pythagoras, knows both aspects. Therefore, the
Indians could not have learnt it from the Old-Babylonians or the Greeks, who
claim to have rediscovered the result only with Pythagoras. India is thus the
cradle of the knowledge of geometry and mathematics."
So, contrary to the European belief that Hindus were
influenced by the Greek geometry, the facts prove that it is the other way
round. Most of the aspects of planar geometry described by Euclid and other
Greek mathematicians were already known to Indians at least 2500 years before
the Greeks. In fact, there are proofs which hint towards the fact Greeks were
influenced by the ancient Hindu Mathematics and Geometry. Bibhuti
Bhushan Datta in his book
"Ancient
Hindu Geometry" states:
"...One who was well versed in that science was
called in ancient India as samkhyajna (the expert of numbers), parimanajna
(the expert in measuring), sama-sutra-niranchaka (Uinform-rope-stretcher),
Shulba-vid (the expert in Shulba) and Shulba-pariprcchaka (the inquirer into
the Shulba). Of these term, viz, 'sama-sutra-niranchaka' perhaps
deserves more particular notice. For we find an almost identical term, 'harpedonaptae'
(rope-stretcher) appearing in the writings of the Greek Democritos (c. 440
BC). It seems to be an instance of Hindu influence on Greek geometry. For the
idea in that Greek term is neither of the Greeks nor of their acknowledged
teachers in the science of geometry, the Egyptians, but it is
characteristically of Hindu origin." The English word 'Geometry' has a
Greek root which itself is derived from the Sanskrit word 'Jyamiti'. In
Sanskrit 'Jya' means an arc or curve and 'Miti' means correct perception or
measurement.
The Sulba Sutras, however, date
from about the eighth century B.C. E. and Dr.
Thibault has shown that
the geometrical theorem of the 47th proposition, Book I, which tradition
ascribes to Pythagoras, was solved by the Hindus at least two centuries earlier,
thus confirming the conclusion of Von
Schroeder that the Greek
philosopher owed his inspiration to India.
(source: History
of Hindu Chemistry,
Volume I p. XXIV ).
***
 A.
L. Basham,
foremost authority on ancient India,
writes in The Wonder That Was
India: A.
L. Basham,
foremost authority on ancient India,
writes in The Wonder That Was
India:
"Medieval Indian mathematicians,
such as Brahmagupta (seventh century), Mahavira (ninth century), and Bhaskara
(twelfth century), made several discoveries which in Europe were not known until
the Renaissance or later. They understood the import of positive and negative
quantities, evolved sound systems of extracting square and cube roots, and could
solve quadratic and certain types of indeterminate equations." Mahavira's most noteworthy contribution is his treatment of fractions for the
first time and his rule for dividing one fraction by another, which did not
appear in Europe until the 16th century.
B.
B.
Dutta
writes: "The use of symbols-letters
of the alphabet to denote unknowns, and equations are the foundations of the
science of algebra. The Hindus were the first to make systematic use of the
letters of the alphabet to denote unknowns. They were also the first to classify
and make a detailed study of equations. Thus they may be said to have given
birth to the modern science of algebra."
The
great Indian mathematician Bhaskaracharya (1150 C.E.) produced extensive
treatises on both plane and spherical trigonometry and algebra, and his works
contain remarkable solutions of problems which were not discovered in Europe
until the seventeenth and eighteenth centuries.
He preceded Newton by over 500
years in the discovery of the principles of differential calculus.
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju
A.
L.
Basham writes further, "The mathematical
implications of zero (sunya) and infinity, never more than vaguely realized by
classical authorities, were fully understood in medieval India. Earlier
mathematicians had taught that X/0 = X, but Bhaskara proved the contrary. He
also established mathematically what had been recognized in Indian theology at
least a millennium earlier: that infinity, however divided, remains infinite,
represented by the equation /X = ."
In the 14th century, Madhava,
isolated in South India, developed a power series
for the arc tangent function, apparently without the use of calculus, allowing
the calculation of to any number of decimal places (since arc tan 1 = /4).
Whether he accomplished this by inventing a system as good as calculus or
without the aid of calculus; either way it is astonishing. Stanley Wolpert
says: " An untutored Kerala mathematician named Madhava developed his own
system of calculus, based on his knowledge of trigonometry around A.D. 1500,
more than a century before either Newton or Liebnitz.
(source: An
Introduction to India - By Stanley Wolpert
p. 195).
By
the fifteenth century C. E. use of the new mathematical concepts from India had
spread all over Europe to Britain, France, Germany, and Italy, among others. A.
L.
Basham states also that
"The debt of the Western world to India in this respect
[the field of mathematics] cannot be overestimated. Most of the great
discoveries and inventions of which Europe is so proud would have been
impossible without a developed system of mathematics, and this in turn would
have been impossible if Europe had been shackled by the unwieldy system of Roman
numerals. The unknown man who devised the new system was, from the world's point
of view, after the Buddha, the most important son of India. His achievement,
though easily taken for granted, was the work of an analytical mind of the first
order, and he deserves much more honor than he has so far received."
 Carl
Friedrich Gauss ( 1777-1855), German scientist
and mathematician, was considered as the "prince of mathematics. He is
frequently called the founder of modern mathematics, who also studied Sanskrit. Carl
Friedrich Gauss ( 1777-1855), German scientist
and mathematician, was considered as the "prince of mathematics. He is
frequently called the founder of modern mathematics, who also studied Sanskrit.
Gauss
"was said to have lamented that Archimedes in the third
century B.C. E. had failed to foresee the Indian system of numeration; how much
more advanced science would have been."
Unfortunately,
Eurocentrism has effectively concealed from the common man the fact that we owe
much in the way of mathematics to ancient India.
In
ancient India, mathematics served as a bridge between understanding material
reality and the spiritual conception. Vedic mathematics differs profoundly from
Greek mathematics in that knowledge for its own sake (for its aesthetic
satisfaction) did not appeal to the Indian mind. The mathematics of the Vedas
lacks the cold, clear, geometric precision of the West; rather, it is cloaked in
the poetic language which so distinguishes the East. Vedic mathematicians
strongly felt that every discipline must have a purpose, and believed that the
ultimate goal of life was to achieve self-realization and love of God and
thereby be released from the cycle of birth and death.
After this period, India was
repeatedly raided by muslims and other rulers and there was a lull in scientific
research. Industrial revolution and Renaissance passed India by. Before
Ramanujan, the only noteworthy mathematician was Sawai
Jai Singh II, who founded the present city of Jaipur in 1727 A.D.
This Hindu king was a great patron of mathematicians and astronomers. He is
known for building observatories (Jantar Mantar)
at Delhi, Jaipur, Ujjain, Varanasi and Mathura. Among the instruments he
designed himself are Samrat Yantra, Ram Yantra and Jai Parkash.
More
recently, intuitive Indian mathematical genius Srinivas
Ramanujan (1887-1920), a friend to all numbers,
was invited to Cambridge by Prof. G. H. Hardy, who recognized his brilliance at
the sight of his first equation solution. Julian Huxley called Ramanujan
"the
greatest mathematician of the century." At
the age of thirty he developed a formula for partitioning any natural number,
which led to the solving of the Waring problem, expressing an integer as the sum
of squares, cubes, or higher powers of a few integers. One day Hardy complained
about the cab number that brought him to visit Ramanujan, "1729" as a
dull number. Ramanujan responded instantly, " No Hardy, 1729 is a wonderful
number! That is the only number which is the sum of two different sets of cubes,
1 and 12, and 9 and 10."
(source: An
Introduction to India - By Stanley Wolpert
p. 195).
Mountstuart
Elphinstone wrote:
"Their geometrical skill is shown among other forms by their demonstrations
of various properties of triangles, especially one which expresses the area in
the terms of the three sides, and was unknown in Europe till published by
Clavius, and by their knowledge of the proportions of the radius to the
circumference of a circle, which they express in a mode peculiar to themselves,
by applying one measure and one unit to the radius and circumference. This
proportion, which is confirmed by the most approved labors of Europeans, was not
known out of India until modern times!"
(source:
History of India - By Mountstuart Elphinstone
London: John Murray Date of Publication: 1849 p. 130).
For more refer to
The
Infinitesimal Calculus: How and Why it Was Imported into Europe - By C. K.
Raju and
Computers, mathematics education, and
the alternative epistemology of the calculus in the Yuktibhâsâ
- By C. K. Raju
***
Srinivas
Ramanujan: A Life of the Genius
 Ramanujan is one of
India´s great intellectual heroes, a
mathematical genius who attributed his brilliance to a personal
relationship with a Hindu Goddess -
Namagiri. His work has been used to help
unravel knots as varied as polymer chemistry and cancer, yet how
he arrived at this theorems is still unknown. By age twelve he had mastered trigonometry so completely
that he was inventing sophisticated theorems that astonished
teachers. Mathematicians have mined his
theorems ever since. They've figured out how to prove them.
They've put them to use. Only recently, a lost bundle of his
notebooks turned up in a Cambridge library. That set mathematics
off on a whole new voyage of discovery. And
where did all this unproven truth come from? Ramanujan was quick
to tell us. He simply prayed to Sarasvathi,
the Goddess of Learning, and she informed him. Ramanujan is one of
India´s great intellectual heroes, a
mathematical genius who attributed his brilliance to a personal
relationship with a Hindu Goddess -
Namagiri. His work has been used to help
unravel knots as varied as polymer chemistry and cancer, yet how
he arrived at this theorems is still unknown. By age twelve he had mastered trigonometry so completely
that he was inventing sophisticated theorems that astonished
teachers. Mathematicians have mined his
theorems ever since. They've figured out how to prove them.
They've put them to use. Only recently, a lost bundle of his
notebooks turned up in a Cambridge library. That set mathematics
off on a whole new voyage of discovery. And
where did all this unproven truth come from? Ramanujan was quick
to tell us. He simply prayed to Sarasvathi,
the Goddess of Learning, and she informed him.
His twenty-one major mathematical papers are
still being plumbed for their secrets, and many of his ideas are
used today in cosmology and computer science. The
unsettling thing is, none of us can find any better way to
explain the magnitude of his eerie brilliance.
(source: http://www.uh.edu/engines/epi495.htm
) John H. Lienhard
(source: The
Man Who Knew Infinity: A Life of the Genius Ramanujan - by
Robert Kanigel)..(source:
Ramanujan
and Computing
the Mathematical face of God). For more on
Ramanuja, refer to chapter on Quotes321_340).
Vedic
Mathematics
"Vedic Mathematics" is the name given
to the ancient system of mathematics, or, to be precise, a unique
technique of calculations based on simple rules and principles,
with which any mathematical problem — be it arithmetic, algebra,
geometry or trigonometry — can be solved. The
system is based on 16 Vedic sutras
or aphorisms, which are actually word-formulae describing natural
ways of solving a whole range of mathematical problems. Some
examples of sutras are "By one more than the one
before", "All from 9 & the last from 10", and
"Vertically & Crosswise". These 16 one-line formulae
originally written in Sanskrit,
which can be easily memorized, enables one to solve long
mathematical problems quickly.
 Born
in the Vedic Age, but buried under centuries of debris, this
remarkable system of calculation was deciphered towards the
beginning of the 20th century, when there was a great interest in
ancient Sanskrit texts, especially in Europe. However, certain
texts called Ganita Sutras,
which contained mathematical deductions, were ignored, because no
one could find any mathematics in them. These texts, it's
believed, bore the germs of what we now know as Vedic Mathematics. Born
in the Vedic Age, but buried under centuries of debris, this
remarkable system of calculation was deciphered towards the
beginning of the 20th century, when there was a great interest in
ancient Sanskrit texts, especially in Europe. However, certain
texts called Ganita Sutras,
which contained mathematical deductions, were ignored, because no
one could find any mathematics in them. These texts, it's
believed, bore the germs of what we now know as Vedic Mathematics.
Vedic math was
rediscovered from the ancient Indian scriptures between 1911 and
1918 by Sri Bharati Krishna Tirthaji (1884-1960), a scholar of
Sanskrit, Mathematics, History and Philosophy. He studied these
ancient texts for years, and after careful investigation was able
to reconstruct a series of mathematical formulae called sutras.
Bharati
Krishna Tirthaji, who was also the former Shankaracharya
of Puri, India, delved into the ancient Vedic texts and
established the techniques of this system in his pioneering work
— Vedic Mathematics (1965),
which is considered the starting point for all work on Vedic math.
It is said that after Bharati Krishna's original 16 volumes of
work expounding the Vedic system were lost, in his final years he
wrote this single volume, which was published five years after his
death.
(source: Vedic
Mathematics - about.com). For more refer to chapter
on Glimpses
VIII and Vedic
Math websites).
***
The
Indic Mathematical tradition
Jean-Étienne
Montucla (1725-1799) French author of Histoire des
mathematiques (1798):
“The ingenious
number-system, which serves as the basis for modern arithmetic,
was used by the Arabs long before it reached
Europe
. It would be a mistake, however, to believe that this invention
is Arabic. There is a great deal of evidence, much of it provided
by the Arabs themselves that this arithmetic originated in
India
.” [Montucla, I, p. 375J.
John
Walls (1616-1703) referred to the nine numerals as Indian figures [Wallis (1695), p. 10]
Cataneo
(1546) le noue figure de
gli Indi, “the nine figures from
India
”. [Smith and Karpinski (1911), p.3
Willichius
(1540) talks of Zyphrae!
Nice, “Indian figures”. [Smith and Karpinski (1911) p.
3]
The
Crafte of Nombrynge (c. 1350), the oldest known
English arithmetical tract: II fforthermore ye most vndirstonde that in this craft ben vsed teen
figurys, as here bene writen for esampul 098 ^ 654321... in the quych we vse teen figwys of Inde. Questio II why Zen figurys of Inde? Soiucio. For as
I have sayd afore thei werefondefrrst in Inde. [D. E. Smith
(1909).
Petrus
of Dada (1291) wrote a commentary on a work entitled Algorismus
by Sacrobosco (John of Halifax, c. 1240), in which he says
the following (which contains a mathematical error): Non
enim omnis numerus
per quascumquefiguras Indorum repraesentatur “Not every
number can be represented in Indian figures”. [Curtze (1.897),
p. 25.
Around the year 1252,
Byzantine monk Maximus Planudes
(1260—1310) composed a work entitled Logistike
Indike (“Indian Arithmetic”) in Greek, or even Psephophoria
kata Indos (“The Indian way of counting”), where he
explains the following: “There are only nine figures.
These are: 123456789 -
[figures given in their Eastern Arabic form]
A sign known as tziphra
can be added to these, which, according to the Indians,
means ‘nothing’. The nine figures themselves are Indian, and tziphra
is written thus: 0”. [B. N., Pans. Ancien
Fonds grec, Ms 2428, f” 186 r”]
Around 1240, Alexandre
de Ville-Dieu composed a manual in verse on written
calculation (algorism). Its title was Carmen
de Algorismo, and it began with the following two lines: Haec
algorismus ars praesens dicitur, in qua Talibus Indorumfruimur bis
quinquefiguris.
“Algorism
is the art by which at present we use those Indian
figures, which number two times five”. [Smith and Karpinski
(1911), p. 11]
In 1202, Leonard
of Pisa (known as Fibonacci), after voyages that took
him to the Near East and Northern Africa, and in particular to
Bejaia (now in Algeria), wrote a tract on arithmetic entitled Liber Abaci (“a tract about the abacus”), in which he
explains the following:
“Cum genitor meus a
patria publicus scriba in duana bugee pro pisanis mercatoribus ad
earn confluentibus preesset, me in pueritia mea ad se uenire
faciens, inspecta utilitate el cornmoditate fiutura, ibi me studio
abaci per aliquot dies stare uoluit et doceri. Vbi a mirabii
magisterio in arte per nouem figuras Indorum introductus. .
. Novem figurae Indorum
hae sun!: cum his itaque novemfiguris. et turn hoc signo o. Quod
arabice zephirum appellatur, scribitur qui libel numerus: “My
father was a public scribe of Bejaia, where he worked for his
country in Customs, defending the interests of Pisan merchants who
made their fortune there. He made me learn how to use the abacus
when I was still a child because he saw how I would benefit from
this in later life. In this way I learned the art of counting
using the nine Indian figures... The nine Indian figures are as
follows:
987654321 - [figures given in
contemporary European cursive form].
“That is why, with these
nine numerals, and with this sign 0, called zephirum
in Arab, one writes all the numbers one
wishes.”[Boncompagni (1857), vol.1]
Rabbi
Abraham Ben MeIr Ben Ezra (1092—1167), after a long
voyage to the East and a period spent in
Italy
, wrote a work in Hebrew entitled: Sefer
ha mispar (“Number Book”), where he explains the basic
rules of written calculation. He uses the first nine letters of
the Hebrew alphabet to represent the nine units. He represents
zero by a little circle and gives it the Hebrew name of galgal
(“wheel”), or, more frequently, sfra
(“void”) from the corresponding Arabic word. However,
all he did was adapt the Indian system to the first nine Hebrew
letters (which he naturally had used since his childhood).
In the introduction, he provides some graphic variations of the
figures, making it clear that they are of Indian origin, after
having explained the place-value system: “That is how the learned
men of India were able to represent any number using
nine shapes which they fashioned themselves specifically to
symbolize the nine units.” (Silberberg (1895), p.2: Smith and
Ginsburg (1918): Steinschneider (1893).
Around the same time, John of Seville
began his Liberalgoarismi de practica arismetrice (“Book of Algoarismi on
practical arithmetic”) with the following:
“Numerus est unitatum
cot/echo, quae qua in infinitum progredilur (multitudo enim
crescit in infinitum), ideo a peritissimis Indis sub quibusdam
regulis et certis lirnitibus infinita numerositas coarcatur, Ut de
infinitis dfinita disciplina traderetur etfuga subtilium rerum sub
alicuius artis certissima Jege ten eretur:
“A number is a collection of units, and because the
collection is infinite (for multiplication can continue
indefinitely), the Indians ingeniously enclosed this infinite
multiplicity within certain rules and limits so that infinity
could be scientifically defined: these strict rules enabled them
to pin down this subtle concept.
[B. N., Paris, Ms. lat. 16 202, p 51: Boncompagni (1857), vol. I,
p. 261
C. 1143, Robert
of
Chester
wrote a work entitled: Algoritmi
de numero Indorum (“Algoritmi: Indian figures”), which
is simply a translation of an Arabic work about Indian arithmetic.
[Karpinski (1915); Wallis (1685). p. 121
C. 1140, Bishop Raymond of
Toledo
gave his patronage to a work written by the converted Jew Juan de
Luna and archdeacon Domingo Gondisalvo: the Liber
Algorismi de numero Indorum (“Book of Algorismi of Indian
figures) which is simply a translation into a Spanish and Latin
version of an Arabic tract on Indian arithmetic. [Boncompagni
(1857), vol. 11
C. 1130, Adelard of
Bath
wrote a work entitled: Algoritmi
de numero Indorum (“Algoritmi: of Indian figures”),
which is simply a translation of an Arabic tract about Indian
calculation. [Boncompagni (1857), vol. Ii
C. 1125, The Benedictine chronicler William
of Malmesbury wrote De
gestis regum Anglorum, in which he related that the Arabs
adopted the Indian figures and transported them to the countries
they conquered, particularly Spain. He goes on to explain that the
monk Gerbert of Aurillac, who was to become Pope Sylvester II (who
died in 1003) and who was immortalized for restoring sciences in
Europe, studied in either
Seville
or
Cordoba
, where he learned about Indian figures and their uses and later
contributed to their circulation in the Christian countries of the
West.
L
Malmesbury (1596), f” 36 r’; Woepcke (1857), p.
35J
Written in 976 in the convent of Albelda (near the town of
Logroño
, in the north of
Spain
) by a monk named Vigila, the Coda
Vigilanus contains the nine numerals in question, but not
zero. The scribe clearly indicates in the text that the figures
are of Indian origin:
“Item
de figuels aritmetice. Scire debemus Indos subtilissimum ingenium
habere et ceteras gentes eis in arithmetica et geometrica et
ceteris liberalibu.c disciplinis concedere. Et hoc manifèstum at
in novem figuris, quibus quibus designant unum quenque gradum
cuiu.slibetgradus. Quatrum hec sunt forma:
9 8 7 6 5 4 3 2 1.
“The same applies to arithmetical figures. It should be noted
that the Indians have an
extremely subtle intelligence, and when it comes to arithmetic,
geometry and other such advanced disciplines, other ideas must
make way for theirs. The best proof of this is the nine figures
with which they represent each number no matter how high. This is
how the figures look:
9 8 7 6 5 4 3 2 1
(source:
The
Indic Mathematical tradition
- By Kosla Vepa).
Top
of Page
Grammar
"Probably
in no other single sphere have Western scholars been so indebted to traditional
India as in that of grammar. "
 According to
Sir
Monier-Williams
(Eng. Sanskrit
scholar 1819-1899):
According to
Sir
Monier-Williams
(Eng. Sanskrit
scholar 1819-1899):
"The Panini grammar reflects the
wondrous capacity of the human brain, which till today no other country has been able to
produce except India."
(source: Hindu
Superiority - By Har Bilas Sarda
p. 229).
Sir William Wilson
Hunter has observed:
"The grammar of Panini
stands supreme among the grammars of the world, alike for its precision of
statement, and for its thorough analysis of the roots of the language and of the
formative principles of words. By employing an algebraic terminology it attains
a sharp succinctness unrivalled in brevity, but at times enigmatical. It
arranges, in logical harmony, the whole phenomena which the Sanskrit language
presents, and stands forth as one of the most splendid achievements of human
invention and industry. So elaborate is the structure, that doubts
have arisen whether its complex rules of formation and phonetic change, its
polysyllabic derivatives, its ten conjugations with their multiform aorists and
long array of tenses, could ever have been the spoken language of a
people."
(source: The
Indian Empire - By
Sir William Wilson Hunter p. 142). For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Panini,
the legendary Sanskrit grammarian of 5th century BC, is the
world's first computational grammarian! Panini's
work, Ashtadhyayi (the Eight-Chaptered book), is considered to
be the most comprehensive scientific grammar ever written for
any language.
"The Panini grammar reflects the
wondrous capacity of the human brain, which till today no other country has been able to
produce except India."
***
The science of linguistics owes much to the
brilliant ancient Sanskrit grammarian Panini, whose 4th century B.C. Ashtadhyayi
("Eight Chapters") was the first scientific analysis of any
alphabet.
 Leonard
Bloomfield (1887-1949) American
linguist and author of Language,
published in 1933) characterization of Panini's
Astadhyayi ("The Eight Books") Leonard
Bloomfield (1887-1949) American
linguist and author of Language,
published in 1933) characterization of Panini's
Astadhyayi ("The Eight Books")
"as one of the
greatest monuments of human intelligence is by no means an exaggeration; no one
who has had even a small acquaintance with that most remarkable book could fail
to agree. In some four thousand sutras or aphorisms - some of them no
more than a single syllable in length - Panini sums up the grammar not only of
his own spoken language, but of that of the Vedic period as well. The work is
the more remarkable when we consider that the author did not write it down but
rather worked it all out of his head, as it were. Panini's disciples committed
the work to memory and in turn passed it on in the same manner to their
disciples; and though the Astadhayayi has long since been committed to writing,
rote memorization of the work, with several of the more important commentaries,
is still the approved method of studying grammar in India today, as indeed is
true of most learning of the traditional culture."
While in the classical world scholars were
dealing with language in a somewhat metaphysical way, the Indians were telling
us what their language actually was, how it worked, and how it was put together.
The methods and techniques for describing the structure of Sanskrit which we
find in Panini have not been substantially bettered to this day in modern
linguistic theory and practice. We today employ many devices in describing
languages that were already known to Panini's first two commentators. The
concept of "zero" which in mathematics is attributed to India, finds
its place also in linguistics.
"It was in India,
however, that there rose a body of knowledge which was destined to revolutionize
European ideas about language. The Hindu grammar taught Europeans to analyze
speech forms; when one compared the constituent parts, the resemblances, which
hitherto had been vaguely recognized, could be set forth with certainty and
precision."
(source: Traditional
India - edited by O. L. Chavarria-Aguilar
refer to chapter on Grammar - By Leonard Bloomfield
Hall - Place of Publication: Englewood Cliffs, NJ Date of
Publication: 1964 p. 109-113).
Ancient Indian work on grammar was not only objective,
systematic, and brilliant than that done in Greece or Rome but is illustrative
of their scientific methods of analysis. Although the date of Panini's grammar,
the Ashtadhyayi,
("Eight Chapters"), which comprises about four thousand sutras or aphorisitic
rules, is uncertain, it is the earliest extant scientific grammar in the world,
having written no later than the fourth century B.C. But prior grammatical
analysis is clearly evidenced by the fact that Panini himself mentions over
sixty predecessors in the field. For example, the sounds represented by the
letters of the alphabet had been properly arranged, vowels and diphthongs
separated from mutes, semivowels, and sibilants, and the sounds had been grouped
into guttturals, palatals, cerebrals, dentals, and labials.
 Panini and other
grammarians, especially Katyayana and Patanjali, carried the work much further,
and by the middle of the second century B.C. Sanskrit had attained a stereotyped
form which remained unaltered for centuries. Whilst Greek grammar tended to be
logical, philosophical and syntactical, Indian grammar was the result of an
empirical investigation of language done with the objectivity of an anatomist
dissecting a body. Panini and other
grammarians, especially Katyayana and Patanjali, carried the work much further,
and by the middle of the second century B.C. Sanskrit had attained a stereotyped
form which remained unaltered for centuries. Whilst Greek grammar tended to be
logical, philosophical and syntactical, Indian grammar was the result of an
empirical investigation of language done with the objectivity of an anatomist
dissecting a body.
At a very early date India began to trace the roots, history, relations and
combinations of words. By the fourth century B.C. she had created for herself
the science of grammar, and produced probably the greatest of all known
grammarians, Panini. The studies of Panini, Patanjali
and Bhartrihari laid the
foundations of philology; and that fascinating science of verbal genetics owed
almost its life in modern times to the rediscovery of Sanskrit.
It is the discovery of Sanskrit by the West and the
study of Indian methods of analysis that revolutionized Western studies of
language and laid the foundation of comparative philology. Panini's Sanskrit grammar, produced in about 300 B.C. E. is the
shortest and the fullest grammar in the world. Until the mid 19th century,
in fact, Panini's great grammar remained the best standard guide to the study of
Sanskrit, an inspiration to students of language everywhere. Even Otto Bohtlingk
and Rudolf Roth, whose monumental Sanskrit-German Dictionary, called the
"St Petersburg Lexicon" because it was published by the Russian
Imperial Academy of Sciences from 1852 to 1875, owed a great debt to Panini's
remarkable "Eight Chapters."
(source: An
Introduction to India - By Stanley Wolpert p. 196).
(For more refer to Electronic
Panini - http://sanskrit.gde.to/all_pdf/aShTAdhyAyI.pdf
and Sanskrit
Learning Tools - http://sanskrit.gde.to/learning_tools/learning_tools.html
and A Software on Sanskrit Grammar based on Panini's
Sutras - http://www.taralabalu.org/panini/greetings.htm).
***
Linguistics
'Sanskrt'
is not a language but a linguistic process.
A L Basham says that the
very science of phonetics arose in Europe only after the discovery' of Sanskrt
and its grammar by the West. (Paanini, the seminal thinker,
constructed the Ashtaadhyaayee - "the Eight Matters to be Studied" in
the 5th cent. BC). His 'structures' constitute a scientific presentation of
grammar, phonetics, etymology, linguistics, etc. all rolled into one, not
excluding the implied "sociology" of listening to, collecting and
statistically evaluating forms of usage in the then spoken language. But, except
for scholars like Naom Chomsky, no one working in linguistics overtly
acknowledges this debt and Paanini has yet to be
admitted to the pantheon of science of which Archimedes, Euclid,
Socrates, Plato, Newton, Einstein, the Quantum Mechanicists, etc. are the
present members. Paanini's work is of immense
importance to modern research in the forms of human speech and,
possibly, in the mapping of the spread of families of languages (not just of the
Indo-European). Such mapping is being currently carried out in the Americas,
very likely without the help of Paanini's ideas, in tracing the waves of
migration of people that were to become "Red Indians" towards the end
of the last Ice Age, from Northeastern Asia, across the Bering Strait, spreading
southwards and across the land as far as Tierra del Fuego (the "Land of
Fire"; "tierra" = dharaa, by the way) at the southern tip of
South America.
One among the major contributions of
the Indian Ancients is the arrangement of letters in
the scripts (aksharamalas) of major Indian languages (Urdu excepted).
That and the mode of having one unique symbol per syllable (and the mode of
formation of compound consonants) whereby, with every letter having a fixed and
invariable pronunciation, the script "is adapted to the expression of every
gradation of sound" (source: Practical Grammar of
the Sanskrit Language - By Sir Monier-Williams
1857).
(source:
Whence and Whither of Indian Science - Can we integrate
with our past and carry on from there? –
Contributed by S. N. Balasubrahmanyam - (Retd) Professor of Organic
Chemistry at the Indian Institute of Science, Bangalore).
Panini
to the rescue
Research
team turns to the "world's first
computational grammarian!".
Panini,
the legendary Sanskrit grammarian of 5th century BC, is the
world's first computational grammarian! Panini's
work, Ashtadhyayi (the Eight-Chaptered book), is considered to
be the most comprehensive scientific grammar ever written for
any language.
According
to Prof Rajeev Sangal, Director of IIIT (Hyderabad) and an expert on language computation, Panini's epic treatise
on grammar came to the rescue of language experts in making
English unambiguous. English is more difficult (as far as
machine translations are concerned) with a high degree of
ambiguity. Some words have different meanings, making the
analysis (to facilitate translations) a difficult process.
Making it disambiguous is quite a task, where Panini's
principles might be of use.
Ashtadhyayi,
the earlier work on descriptive linguistics, consists
of 3,959 sutras (or principles). These highly systemised and
technical principles, some say, marked the rise of classical Sanskrit.
Sampark,
the multi-institute effort launched to produce a translation
engine, enabling users to translate tests from English to
various languages, will use some of the technical aspects
enunciated by Panini. "We looked at alternatives before
choosing Panini," Prof Sangal says. Incidentally, Prof
Sangal co-authored a book, Natural Language Processing - A
Panini Perspective, a few years ago.
Besides
the technical side, Panini would be of great help to researchers
on the translation engine on the language side too. A good
number of words in almost all the Indian languages originate
from Sanskrit. "That is great because Indian languages are
related to each other," Prof Sangal points out.
(source: Panini
to the rescue - thehindu.com). Refer
to chapter on Sanskrit.
Top
of Page
Science
The
revolutionary contents of the Vedas
For
a quick glimpse at what unsung surprises may lie in the Vedas, let us consider
these renditions from the Yajur-veda and Atharva-veda, for instance.
"
O disciple, a student in the science of government, sail
in oceans in steamers, fly in the air in airplanes,
know God the creator through the Vedas, control thy breath through
yoga, through astronomy know the functions of day and night, know
all the Vedas, Rig, Yajur, Sama and Atharva, by means of their
constituent parts."
" Through astronomy, geography,
and geology, go thou to all the different countries of the world
under the sun. Mayest thou attain through good preaching to
statesmanship and artisanship, through medical science obtain
knowledge of all medicinal plants, through hydrostatics learn the
different uses of water, through electricity understand the
working of ever lustrous lightening. Carry out my instructions
willingly." (Yajur-veda
6.21).
 " O royal skilled engineer, construct sea-boats,
propelled on water by our experts, and airplanes, moving and
flying upward, after the clouds that reside in the mid-region,
that fly as the boats move on the sea, that fly high over and
below the watery clouds. Be thou, thereby, prosperous in this
world created by the Omnipresent God, and flier in both air and
lightning." (Yajur-veda
10.19). " O royal skilled engineer, construct sea-boats,
propelled on water by our experts, and airplanes, moving and
flying upward, after the clouds that reside in the mid-region,
that fly as the boats move on the sea, that fly high over and
below the watery clouds. Be thou, thereby, prosperous in this
world created by the Omnipresent God, and flier in both air and
lightning." (Yajur-veda
10.19).
" The atomic energy fissions
the ninety-nine elements, covering its path by the bombardments of
neutrons without let or hindrance. Desirous of stalking the head,
ie. The chief part of the swift power, hidden in the mass of
molecular adjustments of the elements, this atomic energy
approaches it in the very act of fissioning it by the above-noted
bombardment. Herein, verily the scientists know the similar hidden
striking force of the rays of the sun working in the orbit of the
moon." (Atharva-veda
20.41.1-3).
(source: Searching
for Vedic India - By Devamitra Swami p. 155 - 157). For more refer to
chapter on Vimanas
and Advanced Concepts).
Medieval
Arab scholar Sa'id ibn Ahmad al-Andalusi
(1029-1070) wrote in his Tabaqat al-'umam,
one of the earliest books on history of sciences:
"The first nation to have cultivated science is
India. ... India is known for the wisdom of its people. Over many centuries, all
the kings of the past have recognized the ability of the Indians in all the
branches of knowledge".
"The kings of China have stated that the kings of the world are five in
number and all the people of the world are their subjects. They mentioned the
king of China, the king of India, the king of the Turks, the king of the
Persians, and the king of the Romans.
"... They referred to the king of India as the "king of wisdom"
because of the Indians' careful treatment of 'ulum [sciences] and all the
branches of knowledge.
 "The Indians, known to all nations for many centuries, are the metal
[essence] of wisdom, the source of fairness and objectivity. They are people of
sublime pensiveness, universal apologues, and useful and rare inventions.
"The Indians, known to all nations for many centuries, are the metal
[essence] of wisdom, the source of fairness and objectivity. They are people of
sublime pensiveness, universal apologues, and useful and rare inventions.
"... To their credit the Indians have made great strides in the study of
numbers and of geometry. They have acquired immense information and reached the
zenith in their knowledge of the movements of the stars [astronomy] ... After
all that they have surpassed all other peoples in their knowledge of medical
sciences ..."
In his book al-Andalusi goes on to give details of several Indian texts on
astronomy and tells us that the Arab scholars used them in preparing their own
almanacs.
" Ancient Indian theories lacked an empirical
base, but they were brilliant imaginative explanations
of the physical structure of the world, and in a large measure, agreed with the
discoveries of modern physics."
(source: In
the eleventh-century, an important manuscript titled The
Categories of Nations was
authored in Arabic by Said
al-Andalusi, who was a
prolific author and in the powerful position of a judge for the king in Muslim
Spain. A translation and annotation of this was done S.I. Salem and Alok Kumar
and published by University of Texas Press: “Science in the Medieval World”.
This is the first English translation of this eleventh-century manuscript.
Quotes are from Chapter V: “Science in India”).
-
A. L. Basham, Australian Indologist
Two system of Indian thought propound physical theories
suggestively similar to those of Greece. Kanada,
founder of the Vaishehika philosophy, held that the world was composed of atoms
as many in kind as the various elements. The Jains approximated to Democritus by
teaching that all atoms were of the same kind, producing different effects by
diverse modes of combination. Kanada believed light and heat to be varieties of
the same substance; Udayana
taught that all heat comes from the sun; and Vachaspati,
like Newton, interpreted light as composed of minute particles emitted by
substances and striking the eye. Musical notes and intervals were analyzed and
mathematically calculated in the Indian treatises on music. and the Pyrthogorean
Law was formulated by which the number of vibrations, and therefore the pitch of
the note, varies inversely as the length of the string between the point of
attachment and the point of touch.
***
The calculation of eclipses was given by Indian astronomers, refer to verses
from Varahamihira's texts, which give the true reasons for eclipses as the
earth's and moon's shadows (no rAhu kEtu here).
For more refer to History
of Indian Science & Technology.
Top
of Page
Education
The world's first university was
established at Takshashila (northwest region of India) in
approximately 700 B.C. The
Universities in ancient India were entirely residential. It was
considered that a University should contain at least 21 Professors
well versed in Philosophy, Theology and Law; pupils were given free
tuition, free boarding, and students who went to an educational
institution - be the king or a peasant - lived and boarded together.
Ashramas, Viharas and Parishads were
great centers of culture and attracted large numbers.
When
Alexander reached Punjab in 327 BC,
Takshashila, the world's oldest university was already established
as a place of learning. John Keay
in his book India:
a History" writes:
"Students
went there to learn the purest Sanskrit. Kautilya, whose Arthashashtra
is the classic Indian treatise on statecraft, is said to have been
born there in the third century BC. It
was also in Taxila that, in the previous century, Panini
compiled a grammar more comprehensive and scientific than any
dreamed of by Greek grammarians. The
glory for the western world is the library of Alexandria, which
was sanctioned by Ptolemy I Soter, the successor of Alexander of
Macedonia in around 300 BC. While the Maurya
empire was in power in India..."
Dr.
Ernest Binfield Havell
(1861-1934)
principal to the Madras College of Art in the 1890s
and left as principal of the Calcutta College of Art some 20 years
later. He wrote several books, including his book, Indian
Architecture - Its Psychology, Structure and History from the First
Mohammedan Invasion to the Present Day has remarked:
"From the Guru the student would
pass, about the age of sixteen, to one of the great universities
that were the glory of ancient and medieval India. Benares, Taxila,
Vidarbha, Ajanta, Ujjain or Nalanda. Benares was the stronghold of
learning in Buddha's days. Taxila was known at the time of
Alexander's invasion, was known to all of Asia as the leading seat
of Hindu scholarship, renowned above all for its medical school;
Ujjain was held in high repute for astronomy, Ajanta for the
teaching of art. The facade of one of the ruined buildings at Ajanta
suggests the magnificence of these old universities."
(source: Story
of Civilization: Our Oriental Heritage - By Will Durant
MJF Books.1935 p. 556-557).
When Cyrus the Great
(558-530 B.C.),
came to the throne, the city of Takshasila, was already a center of
learning and trade. Young men from Magadha were sent there to finish
their education. The Jataka tales show that young men from all over
the civilized part of India sought education in this city, as well
as from Persia and Mesopotamia.
 The campus
accommodated 10,500 students and
offered over sixty different courses in various fields, such as
science, mathematics, medicine, politics, warfare, astrology,
astronomy, music, religion, and philosophy. The minimum age for
admission was 16 years and students from as far as Babylonia,
Greece, Syria, Arabia, and China came to study at the
university. Taxila,
stood on the banks of the river Vitasa in the northwest of the
Indian subcontinent. The campus
accommodated 10,500 students and
offered over sixty different courses in various fields, such as
science, mathematics, medicine, politics, warfare, astrology,
astronomy, music, religion, and philosophy. The minimum age for
admission was 16 years and students from as far as Babylonia,
Greece, Syria, Arabia, and China came to study at the
university. Taxila,
stood on the banks of the river Vitasa in the northwest of the
Indian subcontinent.
Panini,
the great Sanskrit grammarian, Charaka, the author of famous
treatise on medicine, and
Chanakya, writer of
Artha
Shastra --
these august names are associated with Taxila. Promising
minds from far flung regions converged there to study the Vedas and
all branches of secular knowledge. Takshasila
or Taxila, as the Greeks called it over 2,000 years ago, was at one
of the entrances to the splendor that was India. Its antiquity is
rooted both in epic texts like the Ramayana, Mahabharata and the
other Puranas. The Jakatas are full of references to Taxila - over
100 in fact. We gleam a good many details about it from them.
Mention is made of world-renowned professors who taught the Vedas,
the Kalas, Shilpa, Archery and so on. King Kosala and Jivaka,
the famous physician were students of the University, the latter
learning medicine under Rishi Atreya. Great stress was laid on the
study of Sanskrit and Pali literature.
The University of
Vikramasila accommodated 8,000 people. It was situated on a hill in
Magadha on the banks of the Ganga and flourished for four centuries.
It was destroyed along with Nalanda by the Mohammedan invasion. They
speak of Kulapatis in those times; the technical meaning of the word
is 'one who feeds' and teaches 10,000 students'. Kanva
was one such Kulapati. Kalidasa speaks of the various kinds of
knowledge taught and learnt under the guidance of Kanva.
The University of
Nalanda built in the 4th century BCE was one of the greatest
achievements of ancient India in the field of education. Buddha
visited Nalanda several times during his lifetime. The Chinese
scholar and traveler Hiuen
Tsang stayed
here in the 7th century, and has left an elaborate description of
the excellence, and purity of monastic life practiced here. About
2,000 teachers and 10,000 students from all over the Buddhist world,
lived and studied in this international university. In this first
residential international university of the world, 2,000 teachers
and 10,000 students from all over the Buddhist world lived and
studied here.
 It
had ten thousand students, one hundred lecture-rroms, great
libraries, and six immense blocks of dormitories four stories high;
its observatories, said Yuan
Chwang,
"were lost in the vapors of the morning, and the upper rooms
towered above the clouds." The old Chinese pilgrim loved the
learned monks and shady groves of Nalanda so well he stayed there
for five years. It
had ten thousand students, one hundred lecture-rroms, great
libraries, and six immense blocks of dormitories four stories high;
its observatories, said Yuan
Chwang,
"were lost in the vapors of the morning, and the upper rooms
towered above the clouds." The old Chinese pilgrim loved the
learned monks and shady groves of Nalanda so well he stayed there
for five years.
(source: Story
of Civilization: Our Oriental Heritage - By Will Durant
MJF Books.1935 p. 556-557 and Facets of Indian Culture - By R. Srinivasan
Publisher: Bhartiya Vidya Bhavan p. 237-239).
The
Gupta kings patronized these monasteries, built in old Kushan
architectural style, in a row of cells around a courtyard. Ashoka
and Harshavardhana were some of its most celebrated patrons who
built temples and monasteries here. Recent excavations have
unearthed elaborate structures here. Hiuen Tsang had left ecstatic
accounts of both the ambiance and architecture of this unique
university of ancient times. The Nalanda university counted on its
staff such great thinkers as Nagarjuna,
Aryadeva, Vasubhandu, Asanga, Sthiramati, Dharmapala, Silaphadra,
Santideva and Padmasambhava. The ancient universities were the
sanctuaries of the inner life of the nation. Another large university was
established at Nalanda around 500 B.C. Approximately one mile long
and half-mile wide, this campus housed a large library, called
Dharam gunj (Treasure of Knowledge), that spread over three
buildings, known as Ratna Sagar, Ratnadevi, and Ratnayanjak. Among
other facilities, the university included 300 lecture halls, several
laboratories, and an astronomical research observatory called Ambudharavlehi.
The university used handwritten manuscripts for teaching and
attracted students and staff from many countries, including China,
Korea and Japan. According to the Chinese traveler Hieun Tsang, the
campus housed 10,000 students, 2,000 professors, and a large
administrative staff.
 (source: The Hindu Mind - Fundamentals of Hindu Religion
and Philosophy for All Ages - By Bansi Pandit
B & V
Enterprises, Inc ISBN: 0963479849 p. 302). (source: The Hindu Mind - Fundamentals of Hindu Religion
and Philosophy for All Ages - By Bansi Pandit
B & V
Enterprises, Inc ISBN: 0963479849 p. 302).
These universities were sacked, plundered, looted by the Islamic
onslaught.
According to historian Will
Durant:
"The Mohemmedans destroyed
nearly all the monasteries, Buddhist or Hindu, in northern India.
Nalanda was burned to the ground in 1197 and all its monks were
slaughtered; we can never estimate the abundant life of ancient
India from what these fanatics spared."
(source: Story
of Civilization: Our Oriental Heritage - By Will Durant
MJF Books.1935 p. 558).
The Moghuls
neglected
practical and secular learning, especially the sciences. Throughout
their long rule, no institutions was established comparable to
modern university, although early India had world-famous centers of
learning such as Taxila, Nalanda and Kanchi. Neither the
nobles nor the mullas were stirred into learning...
For more on education, refer to
chapter on Education
in Ancient India).
Top
of Page
Chemistry and metallurgy
Sir Mountstuart
Elphinstone has written:
"Their (Indians) chemical skill is a fact more striking and
more unexpected." "They knew how to prepare sulphuric
acid, nitric acid and muratic acid; the oxide of copper, iron, lead
(of which they had both the red oxide and litharge), tin and zinc:
the suphuret of iron, copper, mercury, and antimony, and arsenic;
the sulphate of copper, zinc and iron; and carbonates of lead and
iron. Their modes of preparing these substances were sometimes
peculiar."
(source: History
of Hindu Chemistry - By
Mountstuart Elphinstone Volume I, Introduction, p. xii
and 54).
Chemistry developed from two source - medicine and
industry. Something has been said about the chemical excellence of cast iron in
ancient India, and about the high industrial development of Gupta Period, when
India was looked to, even by Imperial Rome, as the most skilled of the nations
in such chemical industries as dyeing, tanning, soap-making, glass and cement.
As early as the second century B.C. Nagarjuna
devoted
an entire volume to mercury. By the sixth century Indians were far ahead of
Europe in industrial chemistry; they were masters of calcination, distillation,
sublimation, steaming, fixation, the production of light without heat, the
mixing of anesthetic and soporific powders, and the preparation of metallic
salts, compounds and alloy.

Abundant
evidence available suggests that the ancient Indians were highly skilled in
manufacturing and working with iron and in making and tempering steel. The
analysis of zinc alloys like brass, from archaeological excavations, testify
that the zinc distillation process was known in India as early as 150 B.C.
Indian steel, famous worldwide, is mentioned in history books which tell us that
when Alexander invaded India, Porus, otherwise known as Purushottam,
presented him with thirty pounds of steel, thus indicating its high value.
South
India was a region that was renowned for metallurgy and metalwork in
the old days. In Karnataka, fine steel wires were being produced for
use as strings in musical instruments, at a time when the western
world was using animal gut for the same purpose. Kerala, besides its
large iron smelting furnaces, boasted of special processes such as
the metal mirror of Aranmula. High quality steel from Tamil Nadu was
exported all over the world since Roman times. The
Konasamudram region in Andhra Pradesh was famous for producing the
world renowned Wootz steel - the raw material for King Saladin's
fabled Damascus Sword.
The tempering of
steel was brought in ancient India to a perfection unknown in Europe till our
own times. King Porus is said to have selected, as special valuable gift for
Alexander, not gold or silver, but thirty pounds of steel. The
Muslims took much of this Indian chemical science and industry to the Near East
and Europe; the secret of manufacturing "Damascus" blades, for
example, was taken by Arabs from the Persians, and by the Persians from
India.
Persians considered Indian swords to
be the best, and the phrase, "
Jawabi hind, literally meaning " Indian answer," meant "a cut
with the sword made of Indian steel."
That
the art of metarllurgy was highly developed in ancient India is further
reaffirmed by the fact that the Gypsies, who originated in India, are highly
skilled craftsmen, and it has been suggested that the art of the forge may have
been transmitted to Europe through Gypsies. Steel was manufactured in ancient
India, and it was being exported to China at least by the fifth century A.D.
That the Arabs also imported steel from India is testified to by Al
Kindi, who
wrote in the ninth century.
 Coinage
dating from the 8th Century B.C. to the17th Century A.D. Numismatic evidence of
the advances made by Smelting technology in ancient India. The image of Nataraja
the God of Dance is made of
five metals (Pancha-Dhatu). This technology of mixing two or more metals
and deriving superior alloys has been observed and noted by the Greek Historian Philostratus.
The
Makara (Spire) over Hindu temples were always adorned with brass or gold
toppings (Kamandals). The earliest reference to the advances made in Smelting
technology in India are by Greek historians viz, Philostratus and Ktesias in the
4th century B.C. Coinage
dating from the 8th Century B.C. to the17th Century A.D. Numismatic evidence of
the advances made by Smelting technology in ancient India. The image of Nataraja
the God of Dance is made of
five metals (Pancha-Dhatu). This technology of mixing two or more metals
and deriving superior alloys has been observed and noted by the Greek Historian Philostratus.
The
Makara (Spire) over Hindu temples were always adorned with brass or gold
toppings (Kamandals). The earliest reference to the advances made in Smelting
technology in India are by Greek historians viz, Philostratus and Ktesias in the
4th century B.C.
Great
progress was made in India in mineralogy and metallurgy. The mining and
extensive use of gold, silver, and copper was undertaken in the Indus Valley in
the third century B.C. In the vedic period extensive use was made of copper,
bronze, and brass for household utensils, weapons, and images for worship.
Patanjali, writing in the second century B.C. in his Lohasastra, gives
elaborate directions for many metallurgic and chemical processes, especially the
preparation of metallic salts, alloys, and amalgams, and the extraction,
purification, and assaying of metals. The discovery of aqua regia ( a mixture of
nitric and hydrochloric acid to dissolve gold and platinum) is ascribed to him.
Numerous specimens of weapons made of iron have been excavated, probably
belonging to the fourth century B.C. Iron clamps and the iron stag found at the
Bodhgaya temple point to the knowledge of the process of manufacturing iron as
early as the third century B.C.
Horace Hyman
Wilson
(1786-1860) says: "The Hindus have the art of smelting iron,
of welding it, and of making steel, and have had these arts from
times immemorial."
(source: History
of British India - By James Mill
volume II p. 47).
Saladin's
sword

The finest Damascus
steel was made by a process known only to Indians. The
original Damascus steel-the world's first high-carbon steel-was a product of
India known as wootz. Wootz is the English for ukku in Kannada and Telugu,
meaning steel. Indian steel was used for making swords and armour in Persia and
Arabia in ancient times. Ktesias at the court of Persia (5th c BC) mentions two
swords made of Indian steel which the Persian king presented him. The
pre-Islamic Arab word for sword is 'muhannad' meaning from Hind.
Wootz was produced by carburising chips
of wrought iron in a closed crucible process. "Wrought iron, wood and
carbonaceous matter was placed in a crucible and heated in a current of hot air
till the iron became red hot and plastic. It was then allowed to cool very
slowly (about 24 hours) until it absorbed a fixed amount of carbon, generally
1.2 to 1.8 per cent," said eminent metallurgist Prof. T.R. Anantharaman,
who taught at Banares Hindu University, Varanasi. "When forged into a
blade, the carbides in the steel formed a visible pattern on the surface."
To the sixth century Arab poet Aus b. Hajr the pattern appeared described 'as if
it were the trail of small black ants that had trekked over the steel while it
was still soft'.
The
carbon-bearing material packed in the crucible was a clever way to lower the
melting-point of iron (1535 degrees centigrade). The lower the melting-point the
more carbon got absorbed and high-carbon steel was formed. In the early 1800s,
Europeans tried their hand at reproducing wootz on an industrial scale. Michael
Faraday, the great experimenter and son of a blacksmith, tried to duplicate the
steel by alloying iron with a variety of metals but failed. Some scientists were
successful in forging wootz but they still were not able to reproduce its
characteristics, like the watery mark. "Scientists believe that some other
micro-addition went into it," said Anantharaman. "That is why the
separation of carbide takes place so beautifully and geometrically."
(source:
Lost
knowledge - The Week June 2001).
Hindus made the
best swords in the ancient world, they discovered the process of
making Ukku steel, called Damascus steel by the rest of the world (Damas
meaning water to the Arabs, because of the watery designs on the
blade). These were the best swords in the ancient world,
the strongest and the sharpest, sharper even than Japanese katanas.
Romans, Greeks, Arabs, Persians, Turks, and Chinese imported it. The
original Damascus steel-the world's first high-carbon steel-was a
product of India known as wootz. Wootz is the English for ukku in
Kannada and Telugu, meaning steel. Indian steel was used
for making swords and armor in Persia and Arabia in ancient times.
Ktesias at the court of Persia (5th c BC) mentions two swords made
of Indian steel which the Persian king presented him. The
pre-Islamic Arab word for sword is 'muhannad' meaning from Hind.
So famous were they that the Arabic word for sword was Hindvi - from
Hind.
The
crucible process could have originated in south India and the finest
steel was from the land of Cheras, said K. Rajan,
associate professor of archaeology at Tamil University, Thanjavur,
who explored a 1st century AD trade centre at Kodumanal near
Coimbatore. Rajan's excavations revealed an industrial economy at
Kodumanal.
Pillar
of strength The rustless wonder called the Iron Pillar near the Qutb
Minar at Mehrauli in Delhi did not attract the attention of
scientists till the second quarter of the 19th century.
The
inscription refers to a ruler named Chandra, who had conquered the
Vangas and Vahlikas, and the breeze of whose valour still perfumed
the southern ocean. "The king who answers the description is
none but Samudragupta, the real founder of the Gupta empire,"
said Prof. T.R. Anantharaman, who has authored The
Rustless Wonder. Zinc
metallurgy travelled from India to China and from there to Europe. As
late as 1735, professional chemists in Europe believed that zinc
could not be reduced to metal except in the presence of copper. The
alchemical texts of the mediaeval period show that the tradition was
live in India.
In
1738, William Champion established the Bristol process to produce
metallic zinc in commercial quantities and got a patent for it.
Interestingly, the mediaeval alchemical text Rasaratnasamucchaya
describes the same process, down to adding 1.5 per cent common salt
to the ore.
(source: Saladin's
sword -
The Week - June 24, 2001 - http://netinfo.hypermart.net/telingsteel.htm).
 Nanotechnology
might be of raging interest to scientists world-over now. But
Indians had used nano materials in the 16th century
"unwittingly"
and enabled Arab blacksmiths in making "Damascus steel
sword" which was stronger and sharper. Nanotechnology
might be of raging interest to scientists world-over now. But
Indians had used nano materials in the 16th century
"unwittingly"
and enabled Arab blacksmiths in making "Damascus steel
sword" which was stronger and sharper.
Delivering
a talk on 'The contributions of elemental carbon to the
development of nano science and technology' at the Indian
Institute of Chemical Technology (IICT) Nobel laureate Robert F.
Curl said that carbon nanotechnology was much older than carbon
nano science. For
the
Damascus
sword, Indians produced the raw material -- mined iron ore and
exported it. He said that up to the middle of 18th century, the
steel swords depended on this particular material and when the
mines in
India
stopped, "they lost the technology." The
Damascus
sword when subjected to scrutiny by an electron microscope in 2006
had shown to contain large amounts of nanotubes.
(source:
Nanotechnology
not new to
India
, says Nobel laureate
- the hindu.com).
Refer to
Sciences of the Ancient Hindus: Unlocking Nature in
the Pursuit of Salvation – By Alok Kumar
Iron Pillar - The
Rustless Wonder and a Unique Scientific Phenomenon from Ancient India. A product
of great metallurgical ingenuity
 Traditional
Indian iron and steel are known to have some very special properties such as
resistance to corrosion. This is substantiated by the 1600-year-old, twenty-five
feet high iron pillar next to the Qutub Minar in New Delhi, believed to have
been installed during Chandragupta Maurya's reign.
The famous iron pillar in Delhi belonging to the
fourth-fifth century A.D. is a metallurgical wonder. This huge wrought iron
pillar, 24 feet in height 16.4 inches in diameter at the bottom, and 6 1/2 tons
in weight has stood exposed to tropical sun and rain for fifteen hundred years,
but does not show the least sign of rusting or corrosion. Evidence shows
that the pillar was once a Garuda Stambha
from a Vishnu temple.
This pillar was plundered by Islamic hoards from a temple dedicated to Vishnu
and added as a trophy in the Quwwat al-Islam mosque in Delhi. Made of pure iron, which even today can be produced only
in small quantities by electrolysis. Such a pillar would be most difficult to
make even today. Thus, the pillar defies explanation. Traditional
Indian iron and steel are known to have some very special properties such as
resistance to corrosion. This is substantiated by the 1600-year-old, twenty-five
feet high iron pillar next to the Qutub Minar in New Delhi, believed to have
been installed during Chandragupta Maurya's reign.
The famous iron pillar in Delhi belonging to the
fourth-fifth century A.D. is a metallurgical wonder. This huge wrought iron
pillar, 24 feet in height 16.4 inches in diameter at the bottom, and 6 1/2 tons
in weight has stood exposed to tropical sun and rain for fifteen hundred years,
but does not show the least sign of rusting or corrosion. Evidence shows
that the pillar was once a Garuda Stambha
from a Vishnu temple.
This pillar was plundered by Islamic hoards from a temple dedicated to Vishnu
and added as a trophy in the Quwwat al-Islam mosque in Delhi. Made of pure iron, which even today can be produced only
in small quantities by electrolysis. Such a pillar would be most difficult to
make even today. Thus, the pillar defies explanation.
The pillar is believed to have been made by
forging together a series of disc-shaped iron blooms. Apart from the dimensions another
remarkable aspect of the iron pillar is the absence of corrosion which has been linked to
the composition, the high purity of the wrought iron and the phosphorus content and the
distribution of slag.
Even with today's advances, only four foundries in the
world could make this piece and none are able to keep it rust free. The earliest
known metal expert (2,200 years ago ) was Rishi
Patanjali.
The pillar is a
solid shaft of iron sixteen inches in diameter and 23 feet high.
What is most astounding about it is that it has never rusted even
though it has been exposed to wind and rain for centuries! The
pillar defies explanation, not only for not having rusted, but
because it is apparently made of pure iron, which can only be
produced today in tiny quantities by electrolysis! The technique
used to cast such a gigantic, solid pillar is also a mystery, as it
would be difficult to construct another of this size even today. The
pillar stands as mute testimony to the highly advanced scientific
knowledge that was known in antiquity, and not duplicated until
recent times. Yet still, there is no satisfactory explanation as to
why the pillar has never rusted!
(source: Technology
of the Gods: The Incredible Sciences of the Ancients - By David
Hatcher Childress
p. 80).
 The
Delhi Iron Pillar is a testimony to the high level of skill
achieved by the ancient Indian ironsmiths in the extraction and
processing of iron. The
Delhi Iron Pillar is a testimony to the high level of skill
achieved by the ancient Indian ironsmiths in the extraction and
processing of iron.
Refer to Delhi
Iron Pillar - By Prof. R.
Balasubramaniam - Professor
Department of Materials and Metallurgical Engg Indian Institute of
Technology, Kanpur 208016.
Contributed to this site by
Prof. R. Balasubramaniam. URL: http://home.iitk.ac.in/~bala
The pillar is a
classical example of massive production of high class iron and is
the biggest hand-forged block of iron from antiquity. It is a
demonstration of the high degree of accomplishment in the art of
iron making by ancient Indian iron and steel makers. It has been
said that the Indians were the only non-European people who
manufactured heavy forged pieces of iron and the pieces were of the
size that the European smiths did not learn to make more than one
thousand years later.
The iron pillar near New Delhi is an
outstanding example of Gupta craftmanship. Its total height
inclusive of the capital is 23 feet 8 inches. Its entire weight is 6
tons. The pillar consists of a square abacus, the melon shaped
member and a capital. According to Percy
Brown, this pillar is a
remarkable tribute to the genius and manipulative dexterity of the
Indian worker. Dr. Vincent Smith
says: "It is not many years since the production of such a
pillar would have been an impossibility in the largest foundries of
the world and even now there are comparatively few where a similar
mass of metal could be turned out."
(source: Ancient
India - By V. D. Mahajan p. 543).
The
iron pillar has an inscription in Samskritam written in Brahmi
script. It is a Vishnu Dhvaja on a hill
called Vishnupaada. Installed by King Chandra.
"He, on whose arm fame was inscribed by the sword, when, in
battle in the Vanga countries, he kneaded (and turned) back with
(his) breast the enemies who, uniting together, came against
(him);-he, by whom, having crossed in warfare the seven mouths of
the (river) Sindhu, the Vâhlikas were conquered;-he, by the breezes
of whose prowess the southern ocean is even still perfumed;-
(Line 3.)-He, the remnant of the
great zeal of whose energy, which utterly destroyed (his) enemies,
like (the remnant of the great
glowing heat) of a burned-out fire in a great forest, even now
leaves not the earth; though he, the king, as if wearied, has
quitted this earth, and has gone to the other world, moving in
(bodily) form to the land (of paradise) won by (the merit of has)
actions, (but) remaining on (this) earth by (the memory of his)
fame;-
(L. 5.)-By him, the king,-who attained sole supreme sovereignty in
the world, acquired by his own arm and (enjoyed) for a
very long time; (and) who, having the name of Chandra, carried a
beauty of countenance like (the beauty of) the full-moon,-having in
faith fixed his mind upon (the god) Vishnu, this lofty standard of
the divine Vishnu was set up on the hill (called) Vishnupada."
(source:
yahoogroups
- Indian Civilization).
The
excellent state of preservation of the Iron Pillar, near the Qutb
Minar at Mehrauli in Delhi, despite exposure for 15 centuries to the
elements has amazed corrosion technologists.
 In 1961, the pillar (23 feet and 8
inches, and 6 tonnes) was dug out for chemical treatment and
preservation and reinstalled by embedding the underground part in a
masonry pedestal. Chemical analyses have indicated that the pillar
was astonishingly pure or low in carbon compared with modern
commercial iron. In 1961, the pillar (23 feet and 8
inches, and 6 tonnes) was dug out for chemical treatment and
preservation and reinstalled by embedding the underground part in a
masonry pedestal. Chemical analyses have indicated that the pillar
was astonishingly pure or low in carbon compared with modern
commercial iron.
Traditional
Indian iron and steel are known to have some very special properties
such as resistance to corrosion. This is substantiated by the
1600-year-old, twenty-five feet high iron pillar next to the Qutub
Minar in New Delhi, believed to have been installed during
Chandragupta Maurya's reign. Reports of an international seminar
conducted by the National Metallurgical Laboratory at Jamshedupur in
1963 on the Delhi Iron Pillar, showed that the pillar's corrosion
resistance was not merely the result of some fortuitous
circumstances or Delhi's low humidity, but the
product of great metallurgical ingenuity. In fact,
rust-proof iron has been found in very humid areas as well. A
temple, dedicated to the Goddess Mookambika, is located in Kolur in
Kodachadri Hills in Karnataka - a region which receives a heavy
annual monsoon. A slender iron pillar near the Mookambika temple
stands unrusted despite the severe climatic conditions that it is
subjected to.
(source: Center
for Indian Knowledge Systems -
http://www.ciks.org/methist.html)
The
iron pillar near Qutub Minar at New Delhi is in the news, thanks to the research by Prof.
R. Balasubramaniam of IIT, Kanpur and his team of metallurgists. The
pillar is said to be 1,600 years old. A protective layer of
`misawite' — a compound made up of iron, oxygen and hydrogen on
the steel pillar, which is said to contain phosphorus - is claimed as the
reason for the non-corrosive existence.
(source:
Iron
pillar and nano powder - http://www.hinduonnet.com/thehindu/seta/stories/2002082900020200.htm
All
this historical evidence points to the fact that there existed a
body of knowledge in the fields of metallurgy and metalworking
which, if rediscovered and re-implemented, could revolutionize the
country's iron and steel industry.
The
Periplus
mentions that in the first century
A.D. Indian iron and steel were being exported to Africa and Ethiopia. Indian
metallurgists were well known for their ability to extract metal from ore and
their cast products were highly valued by the Romans, Egyptians, and
Arabs.
Even in technology Indian contribution to world
civilization were significant. The spinning
wheel is an Indian invention, and apart from its economic significance in
reducing the cost of textiles, is one of the first examples of the
belt-transmission of power. The stirrup,
certainly the big-toe stirrup, is of second century B.C. Indian origin. The
ancient blow-gun (nalika), which shot small arrows or iron pellets, may
well have been a forerunner of the air-gun which is supposed to have been
invented by the Europeans in the sixteenth century.
More important is the fact that India supplied the
concept of perpetual motion to European thinking about mechanical power. The
origin of this concept has been traced to Bhaskara, and it was taken to Europe
by the Arabs where it not only helped European engineers to generalize their
concept of mechanical power, but also provoked a process of thinking by analogy
that profoundly influenced Western scientific views. The
Indian idea of perpetual motion is in accordance with the Hindu belief in the
cyclical and self-renewing nature of all things.
In fact, rust-proof iron
has been found in very humid areas as well. A temple, dedicated to the Goddess
Mookambika, is located in Kolur in Kodachadri Hills in Karnataka - a region
which receives a heavy annual monsoon. A slender iron pillar near the Mookambika
temple stands unrusted despite the severe climatic conditions that it is
subjected to.
Galvanising
feat
The oldest among the triad of metallurgical marvels of ancient India is the
extraction of zinc. Zinc is better known as a constituent of brass than a metal
in its own right. Brass with 10 per cent zinc glitters like gold.
The earliest brass objects in India have been unearthed from Taxila (circa 44
BC). They had more than 35 per cent zinc. "This high content of zinc could
be put in only by direct fusion of metallic zinc and copper," said Prof.
T.R. Anantharaman. The other process, which is no more in use, is by heating
zinc ore and copper metal at high temperatures, but the zinc content in brass
then cannot be more than 28 per cent.
Zinc smelting is very complicated as it is a very volatile material. Under
normal pressure it boils at 913 degrees centigrade. To extract zinc from its
oxide, the oxide must be heated to about 1200 degrees in clay retorts. In an
ordinary furnace the zinc gets vapourised, so there has to be a reducing
atmosphere. By an ingenious method of reverse distillation ancient metallurgists
saw to it that there was enough carbon to reduce the heat.
Proof
of the process came from excavations at Zawar in Rajasthan. The Zawar process
consisted of heating zinc in an atmosphere of carbon monoxide in clay retorts
arranged upside down, and collecting zinc vapour in a cooler chamber placed
vertically beneath the retort.
Zinc metallurgy traveled from India to China and from there to Europe. As late
as 1735, professional chemists in Europe believed that zinc could not be reduced
to metal except in the presence of copper. The alchemical texts of the mediaeval
period show that the tradition was live in India.
(source:
Lost
knowledge - The Week June 2001).
***
Manufacture
of Iron and Steel in India
The substance
which seems to have evoked the most scientific and technical
interest in the Britain of the 1790s was the sample of wootz
steel by Dr. Scott to Sir J. Banks, the President of
the British Royal Society. The sample went through thorough
examination and analysis by several experts.
It was found in general to match the best steel then available
in Britain, and according to one user, "purpose of fine
cutlery, and particularly for all edge instruments used for
surgical purposes."
After its being
sent as a sample in 1794 and its examination and analysis in
late 1794 and early 1795, it began to be much in demand, and
some 18 years later the afore-quoted user of steel stated,
"I have to use it for many purposes. If a better steel is
offered to me, I will gladly attend to it; but
the steel of India is decidedly the best I have yet
met with."
Till
well into the 19th Britain produced very little of the steel it
required and imported it
from Sweden, Russia, etc. Partly, Britain lag in steel
production was due to the inferior quality of its iron ore, and
the fuel, i.e. coal, it used. Possibly such lag also resulted
from Britain's backwardness in the comprehensive of processes
and theories on which the production of good steel depended.
Whatever may
have been the understanding in the other European countries
regarding the details of the processes employed in the
manufacture of Indian steel, the British, at the time wootz was
examined and analysed by them, concluded, "that it is made
directly from the ore and consequently it has never been in the
state of wrought iron." Its qualities were thus ascribed to
the quality of the ore from which it came and these qualities
were considered to have little to do with the techniques and
processes employed by the Indian manufacturers. In fact it was
felt that the various cakes of wootz were of uneven texture and
the cause of such imperfection and defects was thought to lie in
the crudeness of the techniques employed.
 It was only
some three decades later that this view was revised. An earlier
revision in fact, even when confronted with contrary evidence as
was made available by other observers of the Indian techniques
and processes, was intellectual impossibility. "That iron
could be converted into cast steel by fusing it in a close
vessel in contact with carbon" was yet to be discovered,
and it was only in 1825 that a British manufacturer "took
out a patent for converting iron into steel by exposing it to
the action of caruretted hydrogen gas in a close vessel, at a
very high temperature, by which means the process of conversion
is completed in a few hours, while by the old method, it was the
work of from 14 to 20 days." It was only
some three decades later that this view was revised. An earlier
revision in fact, even when confronted with contrary evidence as
was made available by other observers of the Indian techniques
and processes, was intellectual impossibility. "That iron
could be converted into cast steel by fusing it in a close
vessel in contact with carbon" was yet to be discovered,
and it was only in 1825 that a British manufacturer "took
out a patent for converting iron into steel by exposing it to
the action of caruretted hydrogen gas in a close vessel, at a
very high temperature, by which means the process of conversion
is completed in a few hours, while by the old method, it was the
work of from 14 to 20 days."
According to
J. M. Heath, founder of the Indian Iron and Steel
Company, and later prominently connected with the development of
steel making in Sheffield, the Indian process appeared to
combine both of the above early 19th century British
discoveries. He observed: "Now it
appears to me that the Indian process combines the principles of
both the above described methods. On elevating the
temperature of the crucible containing pure iron, and dry wood,
and green leaves, an abundant evolution of carburetted hydrogen
gas would take place from the vegetable matter, and as its
escape would be prevented by the luting at the mouth of the
crucible, it would be retained in contact with the iron, which,
at a high temperature, appears from (the above mentioned patent
process) to have a much greater affinity for gaseous than for
conrete carbon; this would greatly shorten the operation, and
probably at a much lower temperature than were the iron in
contact with charcoal powder."
And he added:
"In no other way can I account for the fact that iron is
converted into cast steel by the natives of India, in two hours
and half, with an application of heat, that, in this
country, would be considered quite inadequate to produce such an
effect; while at Sheffield it requires at least four hours to
melt blistered steel in wind-furnaces of the best construction,
although the crucibles in which the steel is melted, are at a
white heat when the metal is put into them, and in the Indian
process, the crucibles are put into the furnace quite
cold."
(source: Indian Science and
Technology in the 18th Century - By Dharampal).
Dr. Ray says: “Coming to comparatively later times, we find
that the Indians were noted for their skill in tempering of steel.
The blades of Damascus were held in high esteem, but it was from
India that the Persians, and, through them, the Arabs learnt the
secret of the operation. The wrought iron pillar close to the
Kutub Minar, near Delhi, which weighs ten tons and is some 1,500
years old, the huge iron girders at Puri, the ornamental gates of
Somnath, and the 24 feet wrought iron gun at Nurvar, are monuments
of a bygone art, and bear silent but eloquent testimony to the
marvelous metallurgical skill attained by the Hindus.”
Regarding the iron pillar, James
Fergusson (1808-1886) says: “It has not, however,
been yet correctly ascertained what its age really is. There is an
inscription upon it, but without a date. From the form of its
alphabet, James Prinsep ascribed it to the third or fourth
century.” Fergusson continues, “Taking A.D 400 as a mean date
– and it certainly is not far from the truth – it opens our
eyes to an unsuspected state of affairs, to find the Hindus at
that age capable of forging a bar of iron larger than any that
have been forged even in Europe up to a very late date, and not
frequently even now. As we find them, however, a few centuries
afterwards using bars as long as this lat in roofing the porch of
the temple at Kanaruc, we must now believe that they were much
more familiar with the use of this metal than they afterwards
became. It is almost equally startling to find that after an
exposure to wind and rain for fourteen centuries it is unrusted,
and the capital and inscription are as clear and as sharp now as
when put up fourteen centuries ago. There is no mistake about the
pillar being of pure iron. General Alexander Cunningham had a bit
of it analyzed in the School of Mines here by Dr. Percy. Both
found it to be pure malleable iron without any alloy.”
Mrs. Charlotte Manning
says: “The superior quality of Hindu steel has long been known,
and it is worthy of record that the celebrated Damascus blades,
have been traced to the workshops of Western India.” She adds:
“Steel manufactured in Kutch enjoys at the present day a
reputation not inferior to that of the steel made in Glasgow and
Sheffield.” “It is probable that ancient India possessed iron
more than sufficient for her wants, and that the Phoenicians
fetched iron with other merchandise from India.”
(source:
Hindu Superiority -
By Har Bilas Sarda
p. 400-404).
Iron
suspension bridges came from Kashmir in India. Papermaking
was commonplace in India and China. European explorers depended
heavily on Indian ship builders.
(source:
Lost
Discoveries: The Ancient Roots of Modern Science - By Dick
Teresi p. 326).
***
Predicting
earthquakes - was
dealt with in detail in the 32nd chapter of Varahamihira's
Brihat Samhita.
The greatness of philosopher,
mathematician and astronomer Varahamihira (505-587 AD) is widely
acknowledged. The Ujjain-born scholar was one of the Navaratnas in
the court of King Vikramaditya Chandragupta II. His works, Pancha-Siddhantika
(The Five Astronomical Canons) and Brihat Samhita (The
Great Compilation), are considered seminal texts on ancient Indian
astronomy and astrology.
What has
astonished scientists and Vedic scholars and has renewed interest
in the Brihat Samhita, are references to unusual
"earthquake clouds" as precursor to earthquakes.
The 32nd chapter
of the manuscript is devoted to signs of earthquakes and
correlates earthquakes with cosmic and planetary influences,
underground water and undersea activities, unusual cloud
formations, and the abnormal behaviour of animals.
Varahamihira
categorises earthquakes into different kinds and says that the
indications of one particular kind will appear in the form of
unusual cloud formations a week before its occurrence: "Its
indications appearing a week before are the following: Huge clouds
resembling blue lily, bees and collyrium in colour, rumbling
pleasantly, and shining with flashes of lightning, will pour down
slender lines of water resembling sharp clouds. An earthquake of
this circle will kill those that are dependent on the seas and
rivers; and it will lead to excessive rains." 1500 years ago
a celebrated astronomer-astrologer-mathematician sought to study
earthquakes on the Indian subcontinent. He drew correlations
between terrestrial earth, the atmosphere and planetary
influences. He described earth as a mass floating on water and
spoke of unusual cloud formations and abnormal animal behaviour as
precursors to earthquakes."
"All in all, this should be
accepted as nothing but astounding."
(source: A temblor from ancient Indian
treasure trove? - Times of India 4/28/01).
***
Diamomds were first mined in India
Knowledge of diamond and the origin
of its many connations starts in India, where it was first mined.
The word most generally used for diamond in Sanskrit is
translitereated as vajra,
"thunderbolt," and indrayudha, "Indra's
weapon." Because Indra is the
warrior god from Vedic scriptures, the foundation of
Hinduism, the thunderbolt symbol indicates much about the Indian
conception of diamond. The flash of lightning is a suitable
comparison for the light thrown off by a fine diamond octahedron
and a diamond's indomitable hardness. Early descriptions of vajra
date to the 4th century BCE which is supported by archaeological
evidence. By that date diamond was a valued material.
 Writings:
The earliest known reference to diamond is a Sanskrit manuscript,
the Arthasastra ("The
Lesson of Profit") by Kautiliya,
a minister to Chandragupta of the Mauryan dynasty in northern
India. The work is dated from 320-296 before the Common Era (BCE).
Kautiliya states "(a diamond that is) big, heavy, capable of
bearing blows, with symmetrical points, capable of scratching
(from the inside) a (glass) vessel (filled with water), revolving
like a spindle and brilliantly shining is excellent. That
(diamond) with points lost, without edges and defective on one
side is bad." Indians recognized the qualities of a fine
diamond octahedron and valued it. Writings:
The earliest known reference to diamond is a Sanskrit manuscript,
the Arthasastra ("The
Lesson of Profit") by Kautiliya,
a minister to Chandragupta of the Mauryan dynasty in northern
India. The work is dated from 320-296 before the Common Era (BCE).
Kautiliya states "(a diamond that is) big, heavy, capable of
bearing blows, with symmetrical points, capable of scratching
(from the inside) a (glass) vessel (filled with water), revolving
like a spindle and brilliantly shining is excellent. That
(diamond) with points lost, without edges and defective on one
side is bad." Indians recognized the qualities of a fine
diamond octahedron and valued it.
(source: American
Museum of Natural History).
The Ratnapradeepika
deals with
diamonds, precious stones and pearls. The word Vajrah
suggests
diamonds in general, and the properties in general. The Maharshis
such as Shounaka have divided diamonds into 4 classes - Khanija,
Kulaja, Shilaja and Kritaka. It also deals with the manufacturing
of artificial diamonds. The salts of alum, borax and ooshara are
regarded as the best ones for this purpose.
(source: Diamonds,
Mechanisms, Weapons of War and Yoga Sutras - By G. R. Joyser
International Academy of Sanskrit Research. p. 1-14).
Pliny, the
Roman writer
(AD 23-79) calls
India "the sole mother of precious stones," and the
"great producer of the most costly gems."
(source: Sanskrit
Civilization - By G. R. Josyer
International Academy of
Sanskrit Researches p. 192).
Arthur George
Parkin, the well known
expert in natural coloring, writes in his work that the process of
coloring thread perfectly with blue and bright red (Manjista) was
known to India from times immemorial and they earned immense money
out of the export trade of colored thread.
(source: Ancient
Indian Culture At A Glance - By Swami Tattwananda
Calcutta, Oxford Book Co. 1962 p. 131).
****
Military science
- Gunpowder
 In regard to military science, the Ramayana and the
Puranas make frequent mention of Shataghnis,
or canons, being placed on forts and used in times of emergency. A canon was
called
"Shataghni"
because it meant the fire weapon that kills one
hundred men at once. They ascribe these
agniyastras, or weapons of fire, to
Visvakarma, the architect of the Vedic epics. Rockets were also Indian
inventions and were used in native armies when Europeans first came into contact
with them. As per Dante's Inferno,
Alexander mentioned in a letter to Aristotle, that terrific flashes of flame
showered on his army in India. The Shukra Neeti is
an ancient text that deals with the manufacture of arms such as rifles and guns.
In The Celtic Druids (pp-115-116),
Godfrey Higgins provides
evidence that Hindus knew of gun powder from the remotest antiquity. In regard to military science, the Ramayana and the
Puranas make frequent mention of Shataghnis,
or canons, being placed on forts and used in times of emergency. A canon was
called
"Shataghni"
because it meant the fire weapon that kills one
hundred men at once. They ascribe these
agniyastras, or weapons of fire, to
Visvakarma, the architect of the Vedic epics. Rockets were also Indian
inventions and were used in native armies when Europeans first came into contact
with them. As per Dante's Inferno,
Alexander mentioned in a letter to Aristotle, that terrific flashes of flame
showered on his army in India. The Shukra Neeti is
an ancient text that deals with the manufacture of arms such as rifles and guns.
In The Celtic Druids (pp-115-116),
Godfrey Higgins provides
evidence that Hindus knew of gun powder from the remotest antiquity.
(source: Proof
of Vedic Culture's Global Existence -
By Stephen Knapp
p. 27-28).
According
to Sir A.
M. Eliot and Heinrich Brunnhofer (a German
Indologist) and Gustav Oppert, all of
whom have stated that ancient Hindus knew the use of gunpowder. Eliot tells us that the Arabs learnt the manufacture of gunpowder
from India, and that before their Indian connection they had used arrows of
naptha. It is also argued that though Persia possessed saltpetre in abundance,
the original home of gunpowder was India. In the light of the above
remarks we can trace the evolution of fire-arms in the ancient India.
(source: German
Indologists: Biographies of Scholars in Indian Studies writing in German
- By Valentine Stache-Rosen. p.92).
(For more information on Military
science please refer to chapter on War
in Ancient India).
***
Vimanas
 “The
ancient Hindus could navigate the air, and not only navigate it, but
fight battles in it like so many war-eagles combating for the
domination of the clouds. To be so perfect in aeronautics, they must
have known all the arts and sciences related to the science,
including the strata and currents of the atmosphere, the relative
temperature, humidity, density and specific gravity of the various
gases...” “The
ancient Hindus could navigate the air, and not only navigate it, but
fight battles in it like so many war-eagles combating for the
domination of the clouds. To be so perfect in aeronautics, they must
have known all the arts and sciences related to the science,
including the strata and currents of the atmosphere, the relative
temperature, humidity, density and specific gravity of the various
gases...”
~ Col. Henry S Olcott (1832
– 1907) American author, attorney,
philosopher, and cofounder of the Theosophical
Society in a lecture in Allahabad, in 1881.
For more information refer to chapter
on Vimanas.
***
The
Process of Making Ice in the East Indies - By Sir Robert Barker
published in 1775
Following is the method that was used to make ice in India as
it was performed at Allahabad and Calcutta. On a large open
plain, 3 or 4 excavations were made, each about 30 feet square
and two deep; the bottoms of which were strewed about eight
inches or a foot thick with sugar-cane, or the stems of the
large Indian corn dried. Upon this bed were placed in rows, near
to each other, a number of small shallow, earthen pans for
containing the water intended to be frozen. These are unglazed,
scarce a quarter of an inch thick, about an inch and a quarter
in depth, and made of an earth so porous, that it was visible,
from the exterior part of the pans, the water had penetrated the
whole substance. Towards the dusk of the evening, they were
filled with soft water, which had been boiled, and then left in
the afore-related situation. The ice-makers attended the pits
usually before the sun was above the horizon, and collected in
baskets what was frozen, by pouring the whole contents of the
pans into them, and thereby retaining the ice, which was daily
conveyed to the grand receptacle or place of preservation,
prepared generally on some high dry situation, by sinking a pit
of fourteen or fifteen feet deep, lined first with straw, and
then with a coarse king of blanketing, where it is beat down
with rammers, till at length its own accumulated cold again
freezes and forms one solid mass. The mouth of the pit is well
secured from the exterior air with straw and blankets, in the
manner of the lining, and a thatched roof is thrown over the
whole.

Ice making in India. It was made in open pans.
***
The spongy nature of the sugar-canes, or stems of the Indian
corn, appears well calculated to give a passage under the pans
to the cold air; which, acting on the exterior parts of the
vessels, may carry off by evaporating a proportion of the heat.
The porous substance of the vessels seems equally well qualified
for the admission of the cold air internally; and their
situation being full of a foot beneath the plane of the ground,
prevents the surface of the water from being ruffled by any
small current of air, and thereby preserves the congealed
particles from disunion. Boiling the water is esteemed a
necessary preparative to this method of congelation.
In effecting which there is also an established mode of
proceeding; the sherbets, creams, or whatever other fluids are
intended to be frozen, are confined in thin silver cups of a
conical form, containing about a pint, with their covers well
luted on with paste, and placed in a large vessel filled with
ice, salt-petre, and common salt, of the two the last an equal
quantity, and a little water to dissolve the ice and combine the
whole. This composition presently freezes the contents of the
cups to the same consistency of our ice creams, etc. in Europe;
but plain water will become so hard as to require a mallet and
knife to break it. The promising advantages of such a discovery
could alone induce the Asiatic to make an attempt of profiting
by so a very short a duration of cold during the night in these
months, and by a well-timed and critical contrivance of securing
this momentary degree of cold, they have procured to themselves
a comfortable refreshment as a recompence, to alleviate, in some
degree, the intense heats of the summer season, which, in some
parts of India, would be scarce supportable, but by the
assistance of this and many other inventions.
(source: Indian Science and
Technology in the 18th Century - By Dharampal p.
169-173).
Top
of Page
Shipbuilding
and Navigation
 The art
of Navigation was born in the river Sindh 6000 years ago. The very word Navigation is
derived from the Sanskrit word
NAV Gatih. The art
of Navigation was born in the river Sindh 6000 years ago. The very word Navigation is
derived from the Sanskrit word
NAV Gatih.
The word navy is also derived from Sanskrit `Nou'.
The Vedic Age was a period of tremendous
wealth and prosperity. The primary sources of knowledge about the Vedic Age is
the Rig Veda. It was a cooperating society based on generate wealth.
Gold
(Hiranya in Sanskrit) was very valuable in this period.
The Rig Veda even refers
to gifts of gold necklaces reaching down to the chest (Hiranya plural). Gold was
smelted from the beds of the rivers Saraswati and Sindhu (Indus).
The
Rig Veda not only refer to the Saraswati as Hiranyavartani, or the path of gold
(and the Sindhu as Hiranmayi or made of gold), it also makes a direct reference
to panned-gold from the Saraswati river bed.
Trade
was also a big part of this civilization. There is overwhelming evidence that
this civilization traded with the Egyptians (with the Sumerians acting as
intermediaries). This directly implies the use of ships.
In fact, the Rig Veda
makes several references to ships used to cross the
"Samudra."
India was a peninsula cut off from the Northern
world by the Himalayas, and from the Eastern and Western, by vast expanses of
water, India had to take to shipping, if she wanted to export her immense
surplus goods. Literature as well as art expresses the life of a people, and
evidences from Indian literature and art prove that in ancient times, India had
developed her own shipping.

Sailor dropping
anchor at Angkorwat, Cambodia.
"Those who believe the
ancient peoples of Asia were incapable of crossing the ocean have completely
lost sight of what the literary sources tell us concerning their ships and their
navigation."
For
more refer to chapter on Greater
India: Suvarnabhumi, Pacific and Sacred
Angkor.
***
 Sardar
Kavalam Madhava Panikkar (1896-1963) Indian
historian, in his book A Survey of Indian
History, was the most impressive in depicting how South
India’s expansion into “further
India” was achieved by the very sea power that
ten centuries later was to open India to colonization by the West: Sardar
Kavalam Madhava Panikkar (1896-1963) Indian
historian, in his book A Survey of Indian
History, was the most impressive in depicting how South
India’s expansion into “further
India” was achieved by the very sea power that
ten centuries later was to open India to colonization by the West:
"From
the first century A.D we witness the strange fact of Hindu or
Hinduised kingdoms in
Annam
, Cochin-China and the islands of the Pacific. The
Ramayana knew of Java and
Sumatra
. Communication by sea between the ports of
South India
and the islands of the Pacific was well established many centuries
before the Christian era."
(source: A
Survey of Indian History - By Sardar Kavalam Madhava Panikkar p.
68 - 69).
For more
refer to Greater
India: Suvarnabhumi, Pacific and Sacred
Angkor.
Baron
Robert von Heine-Geldern (1885 - 1968)
and Gordon F. Ekholm (1909 -
1987) the world's leading
anthropologists, have strongly supported the claim that Indian
ships went all the way to Mexico and Peru centuries before
Columbus.
In the "Civilizations
of Ancient America" they state:
"There
appears to be little doubt but that ship building and navigation
were sufficiently advanced in southern and eastern Asia at the
period in question to have made trans-Pacific voyages possible. In
the third century, horses were exported from India to the Malay
Peninsula and Indo-China, an indication that there must have been
ships of considerable size."
(source: India:
Mother of us All - Edited by Chaman Lal p.
43-44).
 Professor Georg Buehler (1837-1898)
the German Orientalist, had said: Professor Georg Buehler (1837-1898)
the German Orientalist, had said:
"There are passages in ancient Indian works
which prove the early existence of a navigation of the Indian Ocean, and the
somewhat later occurrence of trading voyages undertaken by Hindu merchants to
the shores of the Persian Gulf and its rivers. No commerce can thrive unless
fostered by national shipping."
For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor.
***
History of Indian
Navy
http://armedforces.nic.in/navy/nahist.htm
India's maritime history predates the birth of
western civilization. The world's first tidal dock is believed to have been
built at Lothal around 2300 BC during the Harappan civilization, near
the present day Mangrol harbour on the Gujarat coast.

Ancient Indian
ocean-going ship arriving at Java, from a frieze of the Borobodur stupa.
(image
source: India: A concise history - By Francis Watson
p. 72).
For
more refer to chapter on Greater
India: Suvarnabhumi, Pacific and Sacred
Angkor.
***
The Rig Veda, written
around 2000 BC, credits Varuna with knowledge of the ocean routes commonly used
by ships and describes naval expeditions using hundred-oared ships to subdue
other kingdoms. There is a reference to
Plava,
the side wings of a vessel which give
stability under storm conditions: perhaps the precursor of modern stabilisers.
Similarly, the Atharva Veda mentions boats which were spacious, well constructed
and comfortable.
In Indian mythology, Varuna was the exalted deity to
whom lesser mortals turned for forgiveness of their sins. It is only later that
Indra became known as the King of the Gods, and Varuna was relegated to become
the God of Seas and Rivers. The ocean, recognized as the repository of numerous
treasures, was churned by the Devas and Danavas, the sons of Kashyapa by queens
Aditi and Diti, in order to obtain Amrit, the nectar of immortality. Even today
the invocation at the launching ceremony of a warship is addressed to Aditi.
 The influence of the sea on Indian kingdoms
continued to grow with the passage of time. North-west India came under the
influence of Alexander, who built a harbor at Patala where the Indus branches
into two just before entering the Arabian Sea. His army returned to Mesopotamia
in ships built in Sind. Records show that in the period after his conquest,
Chandragupta
Maurya established an Admiralty Division under a Superintendent of Ships as part
of his war office, with a charter including responsibility for navigation on the
seas, oceans, lakes and rivers.
History
records that Indian ships traded with countries as far as Java and Sumatra, and
available evidence indicates that they were also trading with other countries in
the Pacific and Indian Oceans. Even before Alexander there were references to
India in Greek works, and India had a flourishing trade with Rome.
The
Roman writer Pliny
speaks of Indian traders carrying away large quantities of
gold from Rome, in payment for much-sought exports such as precious stones,
skins, clothes, spices, sandalwood, perfumes, herbs and indigo. The influence of the sea on Indian kingdoms
continued to grow with the passage of time. North-west India came under the
influence of Alexander, who built a harbor at Patala where the Indus branches
into two just before entering the Arabian Sea. His army returned to Mesopotamia
in ships built in Sind. Records show that in the period after his conquest,
Chandragupta
Maurya established an Admiralty Division under a Superintendent of Ships as part
of his war office, with a charter including responsibility for navigation on the
seas, oceans, lakes and rivers.
History
records that Indian ships traded with countries as far as Java and Sumatra, and
available evidence indicates that they were also trading with other countries in
the Pacific and Indian Oceans. Even before Alexander there were references to
India in Greek works, and India had a flourishing trade with Rome.
The
Roman writer Pliny
speaks of Indian traders carrying away large quantities of
gold from Rome, in payment for much-sought exports such as precious stones,
skins, clothes, spices, sandalwood, perfumes, herbs and indigo.
Trade of this volume could not have been conducted
over the centuries without appropriate navigational skills. Two Indian
astronomers of repute,
Aryabhatta
and
Varahamihira,
having accurately mapped the
positions of celestial bodies, developed a method of computing a ship's position
from the stars.
A crude forerunner of the modern
magnetic compass was being used around the fourth or fifth century AD. Called
Matsya Yantra, it comprised an iron fish that floated in a vessel of oil and
pointed North.
 Between the fifth and tenth centuries AD, the
Vijaynagaram and Kalinga kingdoms of southern and eastern India had established
their rule over Malaya, Sumatra and Western Java. The Andaman and Nicobar
Islands then served as an important midway point for trade between the Indian
peninsula and these kingdoms, as also with China. The daily revenue from the
eastern regions in the period 844-848 AD was estimated at 200 maunds (eight
tons) of gold. In the period 984-1042 AD, the Chola kings dispatched great naval
expeditions which occupied parts of Burma, Malaya and Sumatra, while suppressing
the piratical activities of the Sumatran warlords. In
1292 AD,
Marco Polo described Indian ships as " ...built of fir timber,
having a sheath of boards laid over the planking in every part, caulked with
oakum and fastened with iron nails. The bottoms were smeared with a preparation
of quicklime and hemp, pounded together and mixed with oil from a certain tree
which is a better material than pitch." Between the fifth and tenth centuries AD, the
Vijaynagaram and Kalinga kingdoms of southern and eastern India had established
their rule over Malaya, Sumatra and Western Java. The Andaman and Nicobar
Islands then served as an important midway point for trade between the Indian
peninsula and these kingdoms, as also with China. The daily revenue from the
eastern regions in the period 844-848 AD was estimated at 200 maunds (eight
tons) of gold. In the period 984-1042 AD, the Chola kings dispatched great naval
expeditions which occupied parts of Burma, Malaya and Sumatra, while suppressing
the piratical activities of the Sumatran warlords. In
1292 AD,
Marco Polo described Indian ships as " ...built of fir timber,
having a sheath of boards laid over the planking in every part, caulked with
oakum and fastened with iron nails. The bottoms were smeared with a preparation
of quicklime and hemp, pounded together and mixed with oil from a certain tree
which is a better material than pitch."
***
The Rig Veda mentions the two oceans to the east and the west,
(Bay of Bengal and Arabian Sea) just as they
mention ships and maritime trade. Bhujyu, who is one of the main ancestral
figures of the Vedic people, is said in the Rig-Veda (1.116.5) to have been
brought home safely in a ship with a hundred oars. The idea of a houseboat is
implied in several hymns, and so is ocean travel over a period of many days. The
Vedic people were well aware that the Indus and Saraswati poured their water
into the ocean, that the oceans roars, is ever in motion through its waves, and
encircles the land masses.
The picture of the Vedic people as seafaring
merchants meshes perfectly with the archaeological evidence of the Indus-Saraswati
civilization. Apart from foreign artifacts in the Indus cities and Indus
artifacts overseas, there are also steatite seals depicting seaworthy vessels.
The seafaring nature of the Hindus is well known from later sources. King Hiram
of Tyre (Phoenicia) in 975 B.C. traded with India through the port of Ophir (Supara)
near modern Bombay. Harappan seals discovered at several Mesopotamia sites have
been dated to about 2400 B.C.
 A panel found at
Mohenjodaro, depicting a
sailing craft. Vessels were of many types. Their construction is vividly
described in the Yukti Kalpa Taru an ancient Indian text on Ship-building. There is evidence that a compass made by iron
fish floating in a vessel of oil and pointing north was used by mariners. The
typical Harappan seals have been found far a field in Oman, Mesopotamia, and the
Maldives. These finds bear witness to the enthusiastic initiative of the early
Indic peoples as sea faring merchants. A panel found at
Mohenjodaro, depicting a
sailing craft. Vessels were of many types. Their construction is vividly
described in the Yukti Kalpa Taru an ancient Indian text on Ship-building. There is evidence that a compass made by iron
fish floating in a vessel of oil and pointing north was used by mariners. The
typical Harappan seals have been found far a field in Oman, Mesopotamia, and the
Maldives. These finds bear witness to the enthusiastic initiative of the early
Indic peoples as sea faring merchants.
Despite Ancient Concerns about possibly losing caste from crossing the sea,
history reveals India was the foremost maritime nation 2,000 years ago
(meanwhile Europeans were still figuring out the Mediterranean Sea). It had
colonies in Cambodia, Java, Sumatra, Japan, China, Arabia, Egypt and more.
Through Persians and Arabs, India traded with the Roman Empire. The Sanskrit
text, Yukti Kalpa Taru, explains how to build ships, such as the one
depicted in the Ajanta caves. It gives minute details about ship types, sizes
and materials, including suitability of different types of wood. The treatise
also elaborately explains how to decorate and furnish ships so they're
comfortable for passengers.
Yuktikalpataru
gives a detailed classification of ships:
They were two kinds: ordinary (Samanya) ships comprising those used in inland
waters and special (visesa) meant for sea journeys. The largest of these called
Manthara measured 120 cubits in length, 60 in breadth and 60 cubits in height.
During the days of the composition of Yuktikalpataru, it appears that
ship-building was highly advanced. Bhoja has
advised the builders of the sea-faring ships not to join the plants with iron,
as, in the case, the magnetic iron in sea water could expose the ship to danger.
To avoid this risk, he suggests that planks of the bottoms should be held
together with the help of substances other than iron.
According to Marco Polo
an Indian ship could carry crews between 100 to 300. Out of regard for passenger
convenience and comfort, the ships were well furnished and decorated. Gold,
silver, copper and compound of all these substances were generally used for
ornamentation and decoration.
(source: India
Through The Ages: History, Art Culture and Religion - By G. Kuppuram
p. 527-531). For more information, refer to chapters on Seafaring
in Ancient India and War
in Ancient India).
For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Recently, an Indian
scholar, B. C. Chhabra, in his "Vestiges of Indian Culture in Hawaii",
has noticed
certain resemblances between the symbols found in the petroglyohs from the Hawaiian
Islands and those on the Harappan seals. Some of the symbols in the petroglyphs are
described as akin to early Brahmi script.
Will Durant,
eminent American historian, in his book
The Story of
civilizations - Our Oriental Heritage
described India as the most ancient civilization on earth
and he offered many examples of Indian culture throughout the
world. He demonstrated that as early as the ninth century B.C. E. Indians were exploring
the sea routes, reaching out and extending their cultural influences to Mesopotamia,
Arabia, and Egypt.
 The art of shipbuilding and navigation in India and China at the time was
sufficiently advanced for oceanic crossings. Indian ships operating between Indian and
South-east Asian ports were large and well equipped to sail cross the Bay of Bengal. When
the Chinese Buddhist scholar, Fa-hsien, returned from India, his ship carried a crew of more than two hundred
persons and did not sail along the coasts but directly across the ocean. Such ships
were larger than those Columbus used to negotiate the Atlantic a thousand years later.
The art of shipbuilding and navigation in India and China at the time was
sufficiently advanced for oceanic crossings. Indian ships operating between Indian and
South-east Asian ports were large and well equipped to sail cross the Bay of Bengal. When
the Chinese Buddhist scholar, Fa-hsien, returned from India, his ship carried a crew of more than two hundred
persons and did not sail along the coasts but directly across the ocean. Such ships
were larger than those Columbus used to negotiate the Atlantic a thousand years later.
Trade linkages existed between Philippines and with the
powerful Hindu empires in Java and Sumatra. These linkages were venues for
exchanges with Indian culture, including the adoption of syllabic
scripts which are still used by indigenous groups in
Palawan
and Mindoro.
According to the work of mediaeval times, Yukti
Kalpataru, which gives a fund of information
about shipbuilding, India built large vessels from 200 B.C. to the close of the sixteenth
century. A Chinese chronicler mentions ships of Southern Asia that could carry as many as
one thousand persons, and were manned mainly by Malayan crews. They used western winds and
currents in the North Pacific to reach California, sailed south along the coast, and then
returned to Asia with the help of the trade winds, taking a more southerly route, without
however, touching the Polynesian islands. The New Zealand pre historian, S.
Percy
Smith, tries to show in his
Hawaiki - the
Original home of the Maori
that the ancient Polynesian wanderers left
India
as far back as the
fourth century B.C. and were daring mariners who made, more often than not, adventurous
voyages with the definite object of new settlements. A people who reached as far east as
Easter Island could not have missed the great continent ahead of them.
It was probably gold, which initially attracted Indian adventurers and merchants to
Southeast Asia. Southeast Asia was a region broadly referred to by ancient Indians as
Suvarnabhumi (Land of Gold) or Suvarnadvipa (the Island of Gold).
Arab writer
Al Biruni testify that Indians called the whole
Southeast region Suwarndib. Hellenistic geographers knew the area as the Golden
Chersonese. The Chinese called it Kin-Lin; kin means gold. The mariners were probably
looking for gold or were prospecting for precious metals, stones and pearls to cope with
the demand in the centers of ancient civilizations.
"Ships
of size that carried Fahien from India to China (through stormy
China water) were certainly capable of proceeding all the way to
Mexico and Peru by crossing the Pacific. One thousand years before
the birth of Columbus Indian ships were far superior to any made in
Europe upto the 18th century."
(source: The
Civilizations of Ancient America: The Selected Papers of the
XXIXth International Congress of Americanists - edited
Sol Tax 1951).
(Please refer to the chapters
Suvarnabhumi:
Greater India,
War in Ancient India
and
Seafaring in Ancient India
for more information about Indian culture in Southeast Asia.)
He has also further noted that Bombay-built ships
are at least one-fourth cheaper than those built in the docks of England. F.
Balazar Solvyns, a Frenchman, wrote a book titled "Les
Hindous" in 1811.
His remarks are, "In ancient times, the
Indians excelled in the art of constructing vessels, and the present Hindus can
in this respect still offer models to Europe-so much so that the English,
attentive to everything which relates to naval architecture, have borrowed from
the Hindus many improvement which they have adopted with success to their own
shipping.... The Indian vessels unite elegance and utility and are models of
patience and fine workmanship."
(source: http://www.orientalthane.com/speeches/speech_2.htm).
In ancient times the Indians excelled in shipbuilding and even
the English, who were attentive to everything which related to naval architecture, found
early Indian models worth copying. The Indian vessels united elegance and utility, and
were models of fine workmanship.
 Sir
John Malcolm (1769 - 1833) was a Scottish soldier, statesman, and
historian entered the service of the East India Company wrote about Indian
vessels that they: Sir
John Malcolm (1769 - 1833) was a Scottish soldier, statesman, and
historian entered the service of the East India Company wrote about Indian
vessels that they:
"Indian vessels "are so admirably adapted to
the purpose for which they are required that, not withstanding their superior science,
Europeans were unable, during an intercourse with India for two centuries, to suggest or
at least to bring into successful practice one improvement. "
(source:
Journal of Royal Asiatic Society, Vol. I
and India
and World Civilization -
By D P Singhal part
II p. 76 - 77).
For
more refer to chapter on Greater
India: Suvarnabhumi, Pacific
and Sacred
Angkor

 Kavalam
Madhava Panikkar
in his book Asia
and Western Dominance ASIN:
B00005VGEZ published by George Allen, London. 1959 says: Kavalam
Madhava Panikkar
in his book Asia
and Western Dominance ASIN:
B00005VGEZ published by George Allen, London. 1959 says:
"It should be remembered that the
Indian Ocean, including the entire coast of Africa, had been explored centuries
ago by Indian navigators. Indian ships frequented the East African ports and
certainly knew of Madagascar. Vasco da Gama's journey across the Indian Ocean
was guided by an Indian pilot whom the King of Milindi had placed at his
disposal. Fra Mauro preserves the tradition of two voyages from India past the
south end of Africa. He marks the southern cape with the name of Diab and says
that an Indian ship in about 1420 was storm-driven to this point and sailed
westward to 2,000 miles in forty days, without touching land. Fra Mauro had also
spoken himself with a person worthy of confidence who said he had sailed from
India, past Sofala to a place called Garbin on the west coast of Africa. The
Indian Ocean was therefore a charted sea whose routes were known, and as a
navigation achievement long before de Gama."
The
Indian Ocean had from time immemorial been the scene of intense commercial
trade. Indian ships had from the beginning of history sailed across the Arabian
Sea up to the Red Sea ports and maintained intimate cultural and commercial
connections with Egypt, Israel and other countries of the Near East. Long before
Hippalus
disclosed the secret of the monsoon to the Romans, Indian navigators had made
use of these winds and sailed to the Bab-el-Mandeb. To the east, Indian mariners
had gone as far as Borneo and flourishing Indian colonies had existed for over
1,200 years in Malaya, the islands of Indonesia, in Cambodia and Champa and
other areas of the coast. Indian ships from Quilon, made regular journeys to the
South China coast. A long tradition of maritime life was part of the history of
the Peninsular India. The supremacy of India in the waters that washed her coast
was unchallenged till the rise of Arab shipping under the early khalifs.
But
the Arabs and Hindus competed openly, and the idea of 'sovereignty over the sea'
except in the narrow straits was unknown to Asian conception.
Naval fights on any large scale, in the manner of the wars between Carthage and
Rome, seem to have been unknown in India before the arrival of the
Portuguese."
(source: Asia
and Western Dominance ASIN:
B00005VGEZ published by George Allen, London. 1959
p. 28-30). For more on Shipbuilding in
Ancient India, please refer to chapter Seafaring
In Ancient India).
For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Sir Aurel
Stein (1862-1943) a Hungarian and author of several books including Ra`jatarangini:
a chronicle of the kings of Kashmir and Innermost
Asia : detailed report of explorations in Central Asia, Kan-su, and Eastern Iran
carried out and described under the orders of H.M. Indian Government, whose
valuable researches have added greatly to our knowledge of Greater India,
remarks:
"The vast extent of Indian cultural influences, from Central Asia in the
North to tropical Indonesia in the South, and from the Borderlands of Persia to
China and Japan, has shown that ancient India was a radiating center of a
civilization, which by its religious thought, its art and literature, was
destined to leave its deep mark on the races wholly diverse and scattered over
the greater part of Asia."
(source: The
Vision of India - By Sisir Kumar Mitra p. 178 and Main
Currents of Indian Culture - By S. Natarajan p. 50).
 "...an
Indian naval pilot, named Kanha, was hired
by Vasco da Gama to take him to India. Contrary to European portrayals that
Indians knew only coastal navigation, deep-sea shipping had existed in India.
Indian ships had been sailing to islands such as the Andamans, Lakshdweep and
Maldives, around 2,000 years ago. Kautiliya's shastras describe the times that
are good and bad for seafaring. In the medieval period, Arab sailors purchased
their boats in India. The Portuguese also continued to
get their boats from India, and not from Europe. Shipbuilding and exporting was
a major Indian industry, until the British banned it. There is
extensive archival material on the Indian Ocean trade in Greek, Roman, and
Southeast Asian sources." "...an
Indian naval pilot, named Kanha, was hired
by Vasco da Gama to take him to India. Contrary to European portrayals that
Indians knew only coastal navigation, deep-sea shipping had existed in India.
Indian ships had been sailing to islands such as the Andamans, Lakshdweep and
Maldives, around 2,000 years ago. Kautiliya's shastras describe the times that
are good and bad for seafaring. In the medieval period, Arab sailors purchased
their boats in India. The Portuguese also continued to
get their boats from India, and not from Europe. Shipbuilding and exporting was
a major Indian industry, until the British banned it. There is
extensive archival material on the Indian Ocean trade in Greek, Roman, and
Southeast Asian sources."
(source: History
of Indian Science & Technology).
Skilled Seafaring
Men
Catamaran
(from Tamil kattu "to
tie" and maram "wood, tree") is a type of boat or
ship consisting of two hulls joined by a frame. Catamarans were
used by the ancient Tamil Chola dynasty
as early as the 5th century AD for moving their fleets to conquer
such Southeast Asian regions as Cambodia, Burma, Indonesia and
Malaysia) to cross from Polynesia to South America even at the
present time, and the ancient Asians were skilled and enterprising
seafaring men.
(Note:
US Government
recently adopted the ancient
Indian catamaran-making technology to construct fast ships. The
ships, built with technology adapted from ancient Tamil methods to
make catamarans, can travel over 2,500 kms in less than 48 hours,
twice the speed of the regular cargo ships, and carry enough
equipment to support about 5,000 soldiers, the Wall Street Journal
reported yesterday).
(source: U.S.
adopts Indian Catamaran technology -
hindu.com and tribune.com).
For more on Shipbuilding in
Ancient India, please refer to chapter Seafaring
In Ancient India). For
more refer to chapter on Greater
India: Suvarnabhumi, Pacific
and Sacred
Angkor.
Top
of Page
Commerce
Though the Indians have practically no hand now in the
commerce of the world, yet there was a time when they were the
masters of the seaborne trade of Europe, Asia and Africa. They
built ships, navigated the sea, and held in their hands all the
threads of international commerce, whether carried on overland or
by sea.
As their immense wealth was in part
the result of their extensive trade with other countries, so were
the matchless fertility of the Indian soil and the numberless
products of Hindu arts and industries the cause of the enormous
development of the commerce of ancient India.
As poet William Cowper (1731-1800) wrote: “And if a
boundless plenty be the robe,
Trade is a golden girdle of the globe.”
India, which, according to the writer in the Chamber’s
Encyclopedia, “has been celebrated during many ages for its
valuable natural productions, its beautiful manufactures and
costly merchandise,” was, says the Encyclopedia Britannica,
“once the seat of commerce.”
 Mrs.
Charlotte S Manning says: “The indirect
evidence afforded by the presence of Indian products in other
countries coincides with the direct testimony of Sanskrit
literature to establish the fact that the ancient Hindus were a
commercial people.” She concludes: “Enough has now been said
to show that the Hindus have ever been a commercial
people.” Mrs.
Charlotte S Manning says: “The indirect
evidence afforded by the presence of Indian products in other
countries coincides with the direct testimony of Sanskrit
literature to establish the fact that the ancient Hindus were a
commercial people.” She concludes: “Enough has now been said
to show that the Hindus have ever been a commercial
people.”
(source: Ancient
and Medieval India – By Charlotte S Manning volume II
p. 354)
Arnold Hermann Ludwig Heeran
(1760-1842) says: “The Hindus in their most ancient works of poetry are
represented as a commercial people.”
In Sanskrit books, we constantly read of merchants, traders,
and men engrossed in commercial pursuits. Manu
Smriti, one of the oldest books in the world, lays down
laws to govern all commercial disputes having reference to
seaborne traffic as well as the inland and overland commerce.
Traders and merchants are frequently introduced in the Hindu
drama. In Shakuntala we learn
of the importance attached to commerce, where it is stated “that
a merchant named Dhanvriddhi, who had extensive commerce had been
lost at sea and had left a fortune of many millions.” In Nala
and Damyanti, too, we meet with similar incidents. Sir
William Jones is of the opinion that the Hindus “must
have been navigators in the age of Manu, because bottomry (marine
insurance) is mentioned in it.” In the Ramayana,
the practice of bottomry is distinctly noticed. Lord
Mountstuart Elphinstone says: “The Hindus navigated
the ocean as early as the age of Manu’s code because we read in
it of men well acquainted with sea voyages.
According to Max Dunker,
ship-building was known in ancient India about 2000 B.C. It is
thus clear that the Hindus navigated the ocean from the earliest
times and that they carried on trade on an extensive scale with
all the important nations of the Old World.
(source: History of Antiquity – By Max
Dunker volume IV).
With Phoenicia the Indians enjoyed trade from the earliest
times. In the tenth century B.C., Soloman of Israel and Hiram of
Tyre sent ships to India, whence they carried away ivory,
sandalwood, apes, peacocks, gold, silver, precious stones, etc.,
which they purchased from the tribe of Ophir. Now Ptolemy says
there was a country called Abhira at the mouth of the River Indus.
This shows that some people called Abhir must have been living
there in those days. We find a tribe called the “Abhir” still
living in Kathyawar, which must, therefore, be the Ophir tribe
mentioned above. Christian Lassen
(1800-1876) author of Indische Alterthumskunde
vol I p. 354, thinks “Ophir” was a seaport on the south west
coast of India. Mrs. Manning
says it was situated on the western coast of India.
Among the things sent by the Hindus to Solomon and Hiram were
peacocks. Now, these birds were nowhere to be found in those days
except in India, where they have existed from the earliest times.
“We frequently meet in old Sanskrit poetry with sentences like
these: ‘Peacocks unfolding in glittering glory all their green
and gold; ‘peacocks dancing in wild glee at the approach of
rain;’ peacocks around palaces glittering on the garden
walls.’ Ancient sculptures, too show the same delight in
peacocks, as may be seen, for instance, in graceful bas-reliefs on
the gates of Sanchi or in the panels of an ancient palace in
Central India, figured in Colonel Tod’s Rajastathan p. 405.
“The word for peacock in Hebrew is universally admitted to be
foreign; and Gesenius, Sir Emerson
Tennent, and Max Muller
appear to agree with Christian Lassen in holding that this word as
written in Kings and Chronicles is derived from the Sanskrit
language.
With regard to ivory, it was largely used in India, Assyria,
Egypt, Greece and Rome. Elephants are indigenous in India and
Africa, and ivory trade must be either of Indian origin or
African. But the elephants were scarcely known to the ancient
Egyptians, and C Lassen decides that elephants were neither used
nor tamed in ancient Egypt. In ancient India, they were largely
used and tamed. All the kings processions and battles have
elephants mentioned in them. The elephant is the emblem of royalty
and a sign of rank and power. The god Indra, too has his ‘Airawat.’
The Sanskrit name for domestic elephant is ibha, and in the
bazaars of India ibha was the name by which the elephant’s tusks
were sold. In ancient Egypt, ivory was known by the name of ebu.
 It
would be interesting to many to learn that “it was in India that
the Greeks first became acquainted with sugar.” Sugar bears a
name derived from Sanskrit. With the article the name traveled
into Arabia and Persia, and thence became established in the
languages of Europe. It
would be interesting to many to learn that “it was in India that
the Greeks first became acquainted with sugar.” Sugar bears a
name derived from Sanskrit. With the article the name traveled
into Arabia and Persia, and thence became established in the
languages of Europe.
Samuel Maunder (1785-1849) in his The
Treasury of History wrote: “In the reign of
Seleucidas, too, there was an active trade between India and
Syria.” Indian iron and colored cloths and rich apparels were
imported in Babylon and Tyre in ships from India. There were also
commercial routes to Phoenicia, through, Persia. Lord
Mountstuart Elphinstone says: “The extent of the
Indian trade under the first Ptolemies is a well known fact in
history.” Vincent Smith
observes that in the Book of Genesis, “a caravan of camels
loaded with the spices of India and balm and myrrh of Hadramaut.”
John Forbes Royle in his book Ancient
Hindu Medicine p. 119, observes that myrrh is called
bal by the Egyptians, while its Sanskrit name is bola, bearing a
resemblance which leaves no doubt as to its Indian manufacture.
Of the products of the loom, silk was more largely imported
from India into ancient Rome than either in Egypt or Greece. “It
was so alluring the Roman ladies,” says a writer, “that it
sold for its weight in gold.” This is confirmed by the elder
Pliny, who complained that vast sums of money were annually
absorbed by commerce with India. “We are assured on undisputed
authority that the Romans remitted annually to India, a sum
equivalent to 4,000,000 pounds to pay for their investments, and
that in the reign of Ptolemies 125 sails of Indian shipping were
at one time lying in the ports whence Egypt, Syria, and Rome
itself were supplied with the products of India.”
(source: Annals
and Antiquities of Rajasthan: or the Central and Western Rajput
States of India - By
Colonel James Tod p. 221).
Agarthachides, who lived
upwards of 300 years before the time of Periplus, noticed the
active commercial intercourse kept up between Yemen and Pattala
– a seaport town, in Sindh. Pattala in Sanskrit means a
“commercial town.” “which circumstance, if it is true, says Arnold Hermann Ludwig Heeran “would prove the extreme antiquity of the navigation
carried on by the Indus.”
Max Dunker wrote: “Trade existed between
the Indians and Sabaens on the coast of south Arabia before the 10th
century B.C. – the time according to some when Manu lived. In
the days of Alexander, when the Macedonian general, Nearchus, was
entering the Persian Gulf, Muscat was pointed out to him as the
principal mart for Indian products which were transmitted thence
to Assyria.
Egypt was not the only part of Africa with which the Hindus
traded in olden days. The eastern coast of Africa called Zanibar
and the provinces situated on the Red Sea carried on an extensive
trade with ancient India. Myos Hormos, was the chief emporium of
Indian commerce on the Red Sea. Of the trade with Zanzibar, Periplus
gives us pretty full information. He says: “Moreover, indigenous
products such as corn, rice, butter, oil of seasamum, coarse and
fine cotton goods, and cane-honey (sugar) are regularly exported
from the interior of Ariaka (Konkan), and from Barygaza (Baroucha/Broach)
to the opposite coast.”
This trade is also noticed by Arrian, who adds that “this
navigation was regularly managed.”
Arnold Hermann Ludwig Heeran
(1760-1842) says, it is a well known fact that the banians
or Hindu merchants were in the habit of traversing the oceans and
settling in foreign countries. The Eastern countries with which
ancient India traded were chiefly China, Trangangetic Peninsula
and Australia. Professor Heeran says that “the second direction,
which the trade of India took was towards the East, that is, to
the Ultra-Gangetic Peninsula, comprising Ava Mallaca, etc. The
Hindus themselves were in the habit of constructing the vessels in
which they navigated the coast of Coromandel (Cholamandel), and
also made voyages to the Ganges and the peninsula beyond it. These
ships bore different names according to their sizes.
Land Trade
As regards the trade with central and northern Asia, we are
told that “the Indians make expeditions for commercial purposes
into the golden desert Ideste, desert of Cobi, in armed companies
of a thousand or two thousand men. But, according to a report,
they do not return home for three or four years.” The Takhti
Suleman, or the stone tower mentioned by Ptolemy
and Ctesias, was
the starting point for Hindu merchants who went to China.
 Arnold
Hermann Ludwig Heeran
says: “By means of this building it is easy to determine
the particular route as well as the length of time employed by the
Hindu merchants in their journey to China. If we assume Cabul, or
rather Bactria, as their place of departure, the expedition would
take a north-easterly direction as far as the forty-first degree
of the north latitude. It would then have to ascend the mountains,
and so arrive at the stone tower through the defile of Hoshan, or
Owsh. From thence the route led by Cashgar, beyond the mountains
to the borders of the great desert of Cobi, which it traversed
probably through Khotan and Aksu (the Casia and Auxazia of
Ptolemy). From these ancient towns the road lay through Koshotei
to Se-chow, on the frontiers of China, and thence to Pekin, a
place of great antiquity. The whole distance amounts to upwards of
2,500 miles.” Arnold
Hermann Ludwig Heeran
says: “By means of this building it is easy to determine
the particular route as well as the length of time employed by the
Hindu merchants in their journey to China. If we assume Cabul, or
rather Bactria, as their place of departure, the expedition would
take a north-easterly direction as far as the forty-first degree
of the north latitude. It would then have to ascend the mountains,
and so arrive at the stone tower through the defile of Hoshan, or
Owsh. From thence the route led by Cashgar, beyond the mountains
to the borders of the great desert of Cobi, which it traversed
probably through Khotan and Aksu (the Casia and Auxazia of
Ptolemy). From these ancient towns the road lay through Koshotei
to Se-chow, on the frontiers of China, and thence to Pekin, a
place of great antiquity. The whole distance amounts to upwards of
2,500 miles.”
Foreign trade of a nation presupposes development of its
internal trade. Specially is this true of a large country like
India, with its varied products, vast population and high
civilization.
Christian Lassen
(1800-1876) of Paris
considers it remarkable that the Hindus themselves discovered the
rich, luxurious character of India’s products; many of them are
produced in other countries, but remained unnoticed until sought
for by foreigners, where as the most ancient Hindus had a keen
enjoyment in articles of taste and luxury. Rajas and other rich
people delighted in sagacious elephants, swift horses, splendid
peacocks, golden decorations, exquisite perfumes, pungent peppers,
ivory, pearls, gems, gold etc. and consequently caravans were in
continued requisition to carry down these and innumerable other
matters between the north and the south, and the west and the east
of their vast and varied country. These caravans, were met at
border stations and about ports by western caravans or ships bound
to or from Tyre and Egypt or to or from the Persian Gulf and Red
Sea.”
Strabo, Plutarch, and Apollodoras
agree in their statements that India had considerable trade roads
in all directions, with mile stones, and was provided with inns
for travelers. And these “roads” says Heeran, “were planted
with trees and flowers.”
Active internal commerce was carried on in northern India
along the course of the Ganges. Here was the royal highway
extending from Taxila on the Indus to Patliputra (in Bihar) and
which was 10,000 stadia in length, according to Strabo.
Periplus, too, after
saying that “the Ganges and its tributary streams were the grand
commercial routes of northern India,” adds that the “rivers of
the Southern Peninsula also were navigated.”
According to Arrian, the
commercial intercourse between the eastern and western coasts were
carried on in country built ships.
Periplus again says that “in Dachhanabades (Dakshina
Patha in Sanskrit, or the Deccan) there are two very distinguished
and celebrated marts, named Tagara and Pluthama, whence
merchandise was bought down to Barygaza (Barauch). Ozene (Ujjain)
was one of the chief marts for internal traffic, and supplied the
neighboring country with all kinds of merchandise.
The Encyclopedia Britannica
says: “It (India) exported its most valuable produce, its
diamonds, its aromatics, its silks, and its costly manufactures.
The country, which abounded in those expensive luxuries, was
naturally reputed to be the seat of immense riches, and every
romantic tale of its felicity and glory was readily believed. In
the Middle Ages, an extensive commerce with India was still
maintained through the ports of Egypt and the Red Sea; and its
precious produce, imported into Europe by the merchants of Venice,
confirmed the popular opinion of its high refinement and its vast
wealth.”
(source:
Hindu Superiority
– By
Har Bilas Sarda p
405-426). For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Top
of Page
If history proves anything, it
proves that in ancient times, India was the richest country in the
world. The fact that she has always been the cynosure
of all eyes, Asiatic or European, that people of less favored
climes have always cast longing looks on her glittering treasures,
and that the ambition of all conquerors has been to possess India,
prove that she has been reputed to be the richest country in the
world. Her sunny climate, unrivalled fertility, matchless
mineral resources and world-wide exports in ancient times helped
to accumulate in her bosom the wealth which made her the happy
hunting grounds of adventurers and conquerors.
Strabo
(c. 63 BC-3 BC) Greek
historian in his book Geography
II, 5, 12. Describing the location of India and
calls it “the greatest of all nations
and the happiest in lot.”
(source:
India
and World Civilization By D.
P. Singhal Pan Macmillan Limited. 1993. p. 385).
Arnold Hermann Ludwig Heeran
(1760-1842) says: “India has been celebrated
even in the earliest times for her riches.”
The wealth, splendor and prosperity of India had made a
strong impression on the mind of Alexander the Great, and that
when he left Persia for India, he told his army that they were
starting for that “Golden India” where there was endless
wealth, and that what they had seen in Persia was as nothing
compared to the riches of India. Chamber’s
Encyclopedia says” “India has been celebrated
during many ages for its wealth.” The writer of the article
“Hindustan” in the Encyclopedia
Britannica remarks that India “was naturally reputed
to be the seat of immense riches.” Milton
voiced the popular belief when he sang of the wealth of India:
“High on a throne of royal state which far
Outshone the wealth of Ormuz and of Ind (India)
Or where the gorgeous East with richest hand
Showers on her kings barbaric, pearl and gold.”
 Will
Durant 1885-1981) American historian, would like the West to learn
from India, tolerance and gentleness and love for all living things. He had
remarked about the plunder of India thus: Will
Durant 1885-1981) American historian, would like the West to learn
from India, tolerance and gentleness and love for all living things. He had
remarked about the plunder of India thus:
"...It was the
wealth of 18th century India which attracted the commercial pirates of England
and France." "It was this wealth that the East India Company proposed to
appropriate. Already in 1686 its Directors declared their intention to
'establish ....a large, well-grounded, sure English dominion in India for all
time to come."
"The British conquest of
India was the invasion and destruction of a high civilization by a trading
company utterly without scruple or principle, careless of art and greedy of
gain, over-running with fire and sword a country temporarily disordered and
helpless, bribing and murdering, annexing and stealing and beginning that career
of illegal and 'legal' plunder which has now gone on ruthlessly....It was a
simple matter for a group of English buccaneers, armed with the latest European
artillery and morals, to defeat the bows and arrows, the elephants and primitive
musketry of the rajahs, and bringing one Hindu province after another under the
control of the British East India Company."
(source:
The Case for India - By Will Durant p. 7 - 9).
To Shake the
Pagoda Tree
William Finch who
came to India in 1608-11, first described Hindu temples as "pagods,
which are stone images of monstrous men feareful to behold. He
mentioned the temples in Ajmer, "three faire Pagodes richly
wrought with inlayd works, adorned richly
with jewels. Domingo Paes
has left a valuable account of the great Hindu kingdom of
Vijayanagar. He saw outside the city very beautiful pagodas, the
chief among them was the temple of Vitthalasvamin which was begun by
Krsnadeva Raya. Edward Terry, the chaplain to Sir Thomas Roe, King
James's emissary described the temple of Nagarkot as 'most
richly set forth, both scaled and paved with plate of pure
gold." The wealth of the temples stirred Jean Thevenot
imagination and he wrote about the temples of Benares and Puri that
'nothing can be more magnificent than these Pagodes...by reason of
the quantity of gold and many jewels, wherewith they are
adorned."
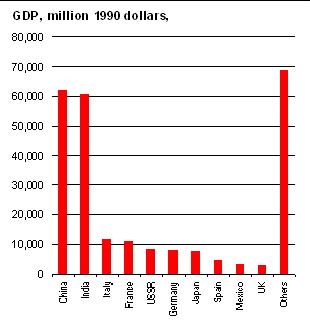
GDP in 1500s.
For
India
's first prime minister Jawaharlal Nehru, the company lay at the root of the
oppression that he had fought against. "The corruption, venality, nepotism,
violence and greed of money of these early generations of British rule in
India
", Nehru thundered in The Discovery of India, "is something
which passes comprehension". Looking back at the company's conquest of
India
, Nehru noted "it is significant that one of the Hindustani words which has
become part of the English language is loot".
***
Most
foreigners came to India in search of her fabulous wealth. No
traveler found India poor until the nineteenth century, but foreign
merchants and adventurers sought her shores for the almost fabulous
wealth, which they could there obtain.
'To
shake the pagoda tree' became a phrase, somewhat similar to our
modern expression 'to strike oil' or
to
get rich quick.
(source:
Much
Maligned Monsters: A History of European Reactions to Indian Art
- By Partha Mitter p. 1 - 45).
 An
idea of the immense wealth of India could be gathered from the
fact that when Sultan Mahmud Ghaznavi destroyed the far
famed temple of Somnath he found such immense riches
and astonishing diamonds cooped up in the single “Idol
of Shiva” that it was found quite impossible to calculate the
value of that booty. An
idea of the immense wealth of India could be gathered from the
fact that when Sultan Mahmud Ghaznavi destroyed the far
famed temple of Somnath he found such immense riches
and astonishing diamonds cooped up in the single “Idol
of Shiva” that it was found quite impossible to calculate the
value of that booty.
Gold, the emblem of wealth, was first found in India. India was
the home of diamonds and other precious stones in ancient times.
Periplus says that “the Greeks used to purchase pieces of gold
from the Indians.” Nelkynda or Neliceram, a port near Calicut on
the Malabar Coast, is said to have been the only market for pearls
in the world in ancient times. The pearls presented by Julius
Ceasar to Servilia, the mother of Brutus, as well as the famous
pearl earring of Cleopatra, were obtained from India. The most
famous diamonds in the world are natives of India. Though the Pitt
(or the Regent as it is now called) weights 136 carats and is
larger in size, yet the Kohinoor, weighing only 106 carats,
hallowed by ages of romantic history, is the most famous diamond
in the world. Both were taken from India by the British. But the
mythological and historical value of the Kohinoor is untold.
The
Priceless Peacock Throne
What
is the costliest single treasure made in the last 1,000 years?
Wrought out of 1150 kg of gold and 230 kg of precious stones,
conservatively in 1999 the throne would be valued at $804 million or
nearly Rs 4.5 billion. In fact when made, it cost twice as much as
the Tajmahal. On the top of each pillar there were to be two
peacocks, thick-set with gems and between each two peacocks a tree
set with rubies and diamonds, emeralds and pearls. The ascent was to
consist of three steps set with jewels of fine water". Of the
11 jewelled recesses formed around it for cushions, the middle one
was intended for the seat it for Emperor. Among the historical
diamonds decorating it were the famous Kohinoor
(186 carats). It was one of the most splendiferous thrones ever
made. it was encrusted with 26,733 precious stones! Ascended by
silver steps, it was sheeted with gold encrusted with emeralds and
rubies. Its back was a peacock's tail of sapphires, pearls and
turquoises. The
throne was completed after seven years of unceasing labour by the
best craftsmen of the empire and was valued at 10 million rupees or
Rs 500 crore today.
(source:
As
priceless as the Peacock Throne
- By K. R. N. Swamy - tribuneindia.com). For more on the
Kohinoor diamond refer to chapter on Glimpses
VIII.
It was the wealth of India that impelled the rude Arabs to
invade the country, and led the half civilized Tartans to overrun
it. It was the wealth of India that attracted Nadir
Shah, the
Portuguese and then the British.
(source:
Hindu Superiority
– By Har Bilas
Sarda p
427 - 430). For more refer to chapters on Islamic
Onslaught and European
Imperialism
India
Was Once the Richest Country in the World
Rev.
Jabez T.
Sunderland
(1842-1936) American born, former President of the
India Information Bureau of America and Editor of Young India (New
York). Author of India,
America and World Brotherhood, and Causes
of Famine in India. He has written glowingly about
India's culture:
 "Another
cause of
India
's impoverishment is the destruction of her manufactures, as the
result of British rule. When the British first appeared on the
scene,
India
was one of the richest countries of the world; indeed it
was her great riches that attracted the British to her shores.
" "Another
cause of
India
's impoverishment is the destruction of her manufactures, as the
result of British rule. When the British first appeared on the
scene,
India
was one of the richest countries of the world; indeed it
was her great riches that attracted the British to her shores.
"
"The
source of her wealth was largely her splendid manufactures. Her
cotton goods, silk goods, shawls, muslins of Dacca, brocades of
Ahmedabad, rugs, pottery of Scind, jewelry, metal work, lapidary
work, were famed not only all over Asia but in all the leading
markets of Northern Africa and of Europe. What has become of those
manufactures? For the most part they are gone, destroyed. Hundreds
of villages and towns of
India
in which they were carried on are now largely or wholly
depopulated, and millions of the people who were supported by them
have been scattered and driven back on the land, to share the
already too scanty living of the poor ryot. What is the
explanation?
Great Britain
wanted
India
's markets. She could not find entrance for British manufactures
so long as
India
was supplied with manufactures of her own. So those of
India
must be sacrificed.
England
had all power in her hands, and so she proceeded to pass tariff
and excise laws that ruined the manufactures of
India
and secured the market for her own goods.
India
would have protected herself if she had been able, by enacting
tariff laws favorable to Indian interests, but she had no power,
she was at the mercy of her conqueror."
(source: The
New Nationalist Movement in
India - By Jabez T Sutherland
- theatlantic.com). Refer to European
Imperialism
 According
to Economist Angus Maddison
(1926 - ) in The World Economy: A
Millennial Perspective, the region that today comprises
the Indian subcontinent held the largest
share of the world's gross domestic product until the beginning of
the 16th century, when it was rivaled by China, and
then again throughout most of the 18th century. According
to Economist Angus Maddison
(1926 - ) in The World Economy: A
Millennial Perspective, the region that today comprises
the Indian subcontinent held the largest
share of the world's gross domestic product until the beginning of
the 16th century, when it was rivaled by China, and
then again throughout most of the 18th century.
At the end of the
16th century, India's great wealth sustained a population of more
than one hundred million people.
In "India, the
Silicon Jewel of the East" (Digital Journal, May 13, 2004), Paul
William Roberts states, "There was an abundance of
arable land, and the state of Indian agriculture compared
favorably with any of the Western European countries. Right down
to the subsistence-oriented peasant, everyone saw a good return on
land and labor. There was a large and vigorous skilled workforce
turning out not just cotton but luxury items for the barons,
courts and ruling classes. Consequently,
the economy produced a fabulous financial surplus."
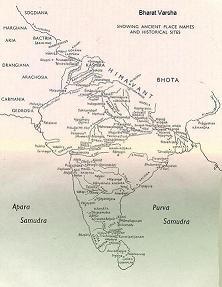 From
the early 18th century until the beginnings of the 19th century,
when India enjoyed a 24.4 % share of the world's gross domestic
product (see table) economic historian Paul Bairoch conforms, the
region enjoyed a 25 % share of the global trade in textiles. It
was the world's leading manufacturer of handicrafts and handloom
textiles. From
the early 18th century until the beginnings of the 19th century,
when India enjoyed a 24.4 % share of the world's gross domestic
product (see table) economic historian Paul Bairoch conforms, the
region enjoyed a 25 % share of the global trade in textiles. It
was the world's leading manufacturer of handicrafts and handloom
textiles.
Bairoch writes, "More
important, there was a large commercialized sector with a highly
sophisticated market and credit structure, manned by a skilful and
in many instances very wealthy commercial class."
Paul William Roberts
adds, "Methods of production and of industrial and commercial
organization could stand comparison with those in vogue in any
other parts of the world. India had developed an indigenous
banking system. Merchant capital had emerged with an elaborate
network of agents, brokers and middlemen. Its bills of exchange
were honored in all the major cities of Asia."
Gross
Domestic Product in Millions of Dollars
|
Year |
1000 |
1500 |
1600 |
1700 |
|
India |
33.8 |
60.5 |
74.3 |
90.8 |
| China |
26.6 |
61.8 |
96.0 |
82.8 |
| Western
Europe |
10.2 |
44.3 |
66.0 |
83.4 |
| World
Total |
116.8 |
247.1 |
329.4 |
371.4 |
Maddison studied
numerous sources and derived historical world gross domestic
product (GDP) totals by assembling evidence on changes in
population, retaining the 1990 international dollar as the
temporal and spatial anchor in the estimation of movements in GDP
and per capita GDP, and filling holes in the evidence with proxy
estimates.
(source: Hinduism
Today - April/May/June 2005 p. 15). For
more refer to chapter on Greater
India: Suvarnabhumi and Sacred
Angkor
Top
of Page
Continue
to Hindu Culture Part II


|


 "From the time of
Megasthenes, who described
India to Greece ca 302 B.C., down to the eighteenth century, India was all a
marvel and a mystery to Europe. Marco Polo (1254-1323) pictured its western
fringe vaguely, Columbus blundered upon America in trying to reach it, Vasco da
Gama sailed around Africa to rediscover it, and merchants spoke rapaciously of
"the wealth of the Indies."
"From the time of
Megasthenes, who described
India to Greece ca 302 B.C., down to the eighteenth century, India was all a
marvel and a mystery to Europe. Marco Polo (1254-1323) pictured its western
fringe vaguely, Columbus blundered upon America in trying to reach it, Vasco da
Gama sailed around Africa to rediscover it, and merchants spoke rapaciously of
"the wealth of the Indies."
 "The
first nation to have cultivated science is India. ... India is known for the
wisdom of its people. Over many centuries, all the kings of the past have
recognized the ability of the Indians in all the branches of knowledge... The
kings of China have stated that the kings of the world are five in number and
all the people of the world are their subjects. They mentioned the king of
China, the king of India, the king of the Turks, the king of the Persians, and
the king of the Romans... They referred to the king of
India as the "king of wisdom" because of the Indians'
careful treatment of ulum (sciences) and all the branches of knowledge. ... The
Indians, known to all nations for many centuries, are the metal (essence) of
wisdom, the source of fairness and objectivity. They are people of sublime
pensiveness, universal apologues, and useful and rare inventions. ... To their
credit the Indians have made great strides in the study of numbers and of
geometry. They have acquired immense information and reached the zenith in their
knowledge of the movements of the stars (astronomy).... After all that they have
surpassed all other peoples in their knowledge of medical sciences.."
"The
first nation to have cultivated science is India. ... India is known for the
wisdom of its people. Over many centuries, all the kings of the past have
recognized the ability of the Indians in all the branches of knowledge... The
kings of China have stated that the kings of the world are five in number and
all the people of the world are their subjects. They mentioned the king of
China, the king of India, the king of the Turks, the king of the Persians, and
the king of the Romans... They referred to the king of
India as the "king of wisdom" because of the Indians'
careful treatment of ulum (sciences) and all the branches of knowledge. ... The
Indians, known to all nations for many centuries, are the metal (essence) of
wisdom, the source of fairness and objectivity. They are people of sublime
pensiveness, universal apologues, and useful and rare inventions. ... To their
credit the Indians have made great strides in the study of numbers and of
geometry. They have acquired immense information and reached the zenith in their
knowledge of the movements of the stars (astronomy).... After all that they have
surpassed all other peoples in their knowledge of medical sciences.." Beginning with the earliest known Indian civilization,
the Indus Valley, with its pottery wheel, cotton textiles, Indus script, and two
wheeled carts, there is a good deal of material and texts to work from. By the
beginning of the third millennium B.C. in India, as in China, Egypt, and
Mesopotamia, scientific development was well advanced. Excavations
carried on at the sites of the Indus civilization have revealed remnants of an
ancient civilization unsurpassed in civil engineering accomplishments,
particularly baths and drainage. Whilst much is
known of the hygienic measures of the period, little is known of the scientific
knowledge upon which it was based. From the town Planning and Great Baths of Indus Valley
it is evidence in the neat arrangement of the major buildings contained in the citadel, including
the placement of a large granary and water tank or bath at right angles to one another.
The lower city, which was tightly packed with residential units, was also constructed on a
grid pattern consisting of a number of blocks separated by major cross streets.
Baked-brick houses faced the street, and domestic life was centered around an enclosed
courtyard.
The cities had an elaborate public drainage system, Sanitation was provided through an
extensive system of covered drains running the length of the main streets and connected by
chutes with most residences.
Beginning with the earliest known Indian civilization,
the Indus Valley, with its pottery wheel, cotton textiles, Indus script, and two
wheeled carts, there is a good deal of material and texts to work from. By the
beginning of the third millennium B.C. in India, as in China, Egypt, and
Mesopotamia, scientific development was well advanced. Excavations
carried on at the sites of the Indus civilization have revealed remnants of an
ancient civilization unsurpassed in civil engineering accomplishments,
particularly baths and drainage. Whilst much is
known of the hygienic measures of the period, little is known of the scientific
knowledge upon which it was based. From the town Planning and Great Baths of Indus Valley
it is evidence in the neat arrangement of the major buildings contained in the citadel, including
the placement of a large granary and water tank or bath at right angles to one another.
The lower city, which was tightly packed with residential units, was also constructed on a
grid pattern consisting of a number of blocks separated by major cross streets.
Baked-brick houses faced the street, and domestic life was centered around an enclosed
courtyard.
The cities had an elaborate public drainage system, Sanitation was provided through an
extensive system of covered drains running the length of the main streets and connected by
chutes with most residences.  They
had wide main streets and were magnificently laid out in grid form, reflecting
careful town planning. They had sewers, municipal water systems, public baths,
and well-fortified citadels. The private houses were well built, of fine solid
baked bricks which have not crumbled over the centuries. Many of them were two
stories high, and had seat latrines and chutes for refuse. Homes were built
around courtyards. The people of the Indus Valley civilization had an advanced
technology. They knew how to make cotton cloth and copper and bronze castings
and forgings. Some of
their art objects have a wonderful simple realism. The torso of one small
dancing figure is so unbelievably alive that one can almost feel the easy
muscles at work under the smooth skin.
They
had wide main streets and were magnificently laid out in grid form, reflecting
careful town planning. They had sewers, municipal water systems, public baths,
and well-fortified citadels. The private houses were well built, of fine solid
baked bricks which have not crumbled over the centuries. Many of them were two
stories high, and had seat latrines and chutes for refuse. Homes were built
around courtyards. The people of the Indus Valley civilization had an advanced
technology. They knew how to make cotton cloth and copper and bronze castings
and forgings. Some of
their art objects have a wonderful simple realism. The torso of one small
dancing figure is so unbelievably alive that one can almost feel the easy
muscles at work under the smooth skin.  In ancient India, as in Greece, there was much
speculative thought about astronomy, mathematics, physics, and biology. But
mathematics and mysticism were inextricably mixed in early Greek thought, and
Greek belief in magic, divination and oracles was perhaps more pronounced than
its counterpart in India.
In ancient India, as in Greece, there was much
speculative thought about astronomy, mathematics, physics, and biology. But
mathematics and mysticism were inextricably mixed in early Greek thought, and
Greek belief in magic, divination and oracles was perhaps more pronounced than
its counterpart in India. The spirit of scientific enquiry and a rigorous
correlation of cause and effect in explaining natural phenomenon were
particularly evident in ancient India. The connection between Indian philosophy
and medicine, mathematics, astronomy, and technology is, strangely enough seldom
realized much less recognized.
The spirit of scientific enquiry and a rigorous
correlation of cause and effect in explaining natural phenomenon were
particularly evident in ancient India. The connection between Indian philosophy
and medicine, mathematics, astronomy, and technology is, strangely enough seldom
realized much less recognized. The
beginnings of algebra can be traced to the constructional geometry of the Vedic
priests, which are preserved in the Shulba Sutras. Exact measurements,
orientations, and different geometrical shapes for the altars and arenas used
for the religious functions (yajnas), which occupy an important part of the
Vedic religious culture, are described in the Shulba Sutras. Many of these
calculations employ the geometrical formula known as the Pythagorean theorem.
The
beginnings of algebra can be traced to the constructional geometry of the Vedic
priests, which are preserved in the Shulba Sutras. Exact measurements,
orientations, and different geometrical shapes for the altars and arenas used
for the religious functions (yajnas), which occupy an important part of the
Vedic religious culture, are described in the Shulba Sutras. Many of these
calculations employ the geometrical formula known as the Pythagorean theorem. 



 The transcendence of time is
the aim of every Indian spiritual tradition. Time is often presented as an eternal wheel
that binds the soul to a mortal existence of ignorance and suffering. "Release"
from time's fateful wheel is termed
moksha, and an advanced ascetic may be called
kala-attita
(' he who has transcended time').
The transcendence of time is
the aim of every Indian spiritual tradition. Time is often presented as an eternal wheel
that binds the soul to a mortal existence of ignorance and suffering. "Release"
from time's fateful wheel is termed
moksha, and an advanced ascetic may be called
kala-attita
(' he who has transcended time').
 Dr.
Carl Sagan
Dr.
Carl Sagan

 Princeton
University’s Paul Steinhardt and Cambridge
University’s Neil Turok, have recently
developed The Cyclical Model.
Princeton
University’s Paul Steinhardt and Cambridge
University’s Neil Turok, have recently
developed The Cyclical Model.  Dr.
Alok Kumar professor of Physics at the State University of New York
at Oswego and author of the new book, Sciences of the
Ancient Hindus has observed:
Dr.
Alok Kumar professor of Physics at the State University of New York
at Oswego and author of the new book, Sciences of the
Ancient Hindus has observed:


 The late scientist,
The late scientist,





 A 9th century Hindu scripture, The Mahapurana
by Jinasena claims the something as modern as the following:
(translation from [5])
A 9th century Hindu scripture, The Mahapurana
by Jinasena claims the something as modern as the following:
(translation from [5]) In the realm of physics, remarkable contributions
have been made by Indian scientists.
Some hint at the theory may be contained in the views of Uddalaka
Aruni, preserved in the Chandogya Upanishad.
Uddalaka says: "matter was at first a chaotic mass, like the juices of
various trees indiscriminately blended together in honey. In order to develop
names-and-forms, to discriminate things from one another, or to set them in
order, the universal spirit came not in its universal form but as the living,
principle, and entered into Fire, Water and Earth. After separating their
component but qualitatively distinct parts (dhatus), it made numerous new
combinations of them. By propounding the theory of combination and separation of
particles, Uddalaka anticipated the atomic theory of Kannada.'
In the realm of physics, remarkable contributions
have been made by Indian scientists.
Some hint at the theory may be contained in the views of Uddalaka
Aruni, preserved in the Chandogya Upanishad.
Uddalaka says: "matter was at first a chaotic mass, like the juices of
various trees indiscriminately blended together in honey. In order to develop
names-and-forms, to discriminate things from one another, or to set them in
order, the universal spirit came not in its universal form but as the living,
principle, and entered into Fire, Water and Earth. After separating their
component but qualitatively distinct parts (dhatus), it made numerous new
combinations of them. By propounding the theory of combination and separation of
particles, Uddalaka anticipated the atomic theory of Kannada.' The believed that energy was indestructible and
thus anticipated the law of conservation and energy. Heat and light were viewed
as only different forms of the same essential substance. One of the scientists
succeeded in suggesting a scientific explanation of the phenomenon of ebullition
and rarefaction in evaporation. They were familiar with refraction and chemical
effects of light rays, causes of translucency, opacity and shadows. They evolved
the formula that the angle of incidence was equal to the angle of reflection.
The believed that energy was indestructible and
thus anticipated the law of conservation and energy. Heat and light were viewed
as only different forms of the same essential substance. One of the scientists
succeeded in suggesting a scientific explanation of the phenomenon of ebullition
and rarefaction in evaporation. They were familiar with refraction and chemical
effects of light rays, causes of translucency, opacity and shadows. They evolved
the formula that the angle of incidence was equal to the angle of reflection. Only
seven years after the first successful atom bomb blast in New Mexico, Dr.
Oppenheimer of the Manhattan Project, who was
familiar with ancient Sanskrit literature, was giving a lecture at Rochester
University. During the question and answer period a student asked a question to
which Oppenheimer gave a strangely qualified answer:
Only
seven years after the first successful atom bomb blast in New Mexico, Dr.
Oppenheimer of the Manhattan Project, who was
familiar with ancient Sanskrit literature, was giving a lecture at Rochester
University. During the question and answer period a student asked a question to
which Oppenheimer gave a strangely qualified answer: Edward
Teller (1908-2003)
Edward
Teller (1908-2003) 
 In
In
 Highly intellectual and given to abstract thinking as
they were, one would expect the ancient Indians to excel in mathematics. Ancient Indians developed a system of mathematics far
superior, to that of the Greeks. Ancient Vedic mathematicians devised sutras for
solving mathematical problems with apparent ease. Among the most vital parts of our heritage are
the numerals and the decimal system. The miscalled "Arabic" numerals
are found on the Rock Edicts of Ashoka (250 B.C.), a thousand years before their
occurrence in Arabic literature. Hindsaa
(numerals) in Arabic means from India. Jawaharlal Nehru has said, " The
clumsy method of using a counting frame and the use of Roman and such like
numerals had long retarded progress when the ten Indian numerals, including the
zero sign, liberated the human mind from these restrictions and threw a flood of
light on the behavior of numbers."
Highly intellectual and given to abstract thinking as
they were, one would expect the ancient Indians to excel in mathematics. Ancient Indians developed a system of mathematics far
superior, to that of the Greeks. Ancient Vedic mathematicians devised sutras for
solving mathematical problems with apparent ease. Among the most vital parts of our heritage are
the numerals and the decimal system. The miscalled "Arabic" numerals
are found on the Rock Edicts of Ashoka (250 B.C.), a thousand years before their
occurrence in Arabic literature. Hindsaa
(numerals) in Arabic means from India. Jawaharlal Nehru has said, " The
clumsy method of using a counting frame and the use of Roman and such like
numerals had long retarded progress when the ten Indian numerals, including the
zero sign, liberated the human mind from these restrictions and threw a flood of
light on the behavior of numbers."  Said the great and magnanimous
Said the great and magnanimous  John
D Barrow (1952 - )
John
D Barrow (1952 - ) "The Western world owes
a great deal to India for a simple invention. It was developed by an unknown
Indian more than 1500 years ago. Without it most of the great discoveries and
inventions (including computers) of western civilization would never have come
about. This invention was the decimal system of numerals - nine digits and a
zero. The science and technology of today (including the computers) could not
have developed if we had only the Roman system of numerals. That system is too
clumsy to be used as a scientific too. Today we take the decimal system for
granted. We don't think about how brilliant the man who invented zero must have
been. Yet without zero we could not assign a place value to the digits. That
ancient mathematician, whoever, he was, deserves much honor."
"The Western world owes
a great deal to India for a simple invention. It was developed by an unknown
Indian more than 1500 years ago. Without it most of the great discoveries and
inventions (including computers) of western civilization would never have come
about. This invention was the decimal system of numerals - nine digits and a
zero. The science and technology of today (including the computers) could not
have developed if we had only the Roman system of numerals. That system is too
clumsy to be used as a scientific too. Today we take the decimal system for
granted. We don't think about how brilliant the man who invented zero must have
been. Yet without zero we could not assign a place value to the digits. That
ancient mathematician, whoever, he was, deserves much honor."




 The
Jesuits also needed these texts to understand the local
customs and how the dates of traditional festivals were fixed by
Indians using the local calendar (“panchânga”). How the
mathematics given in these Indian ancient texts subsequently
diffused into
The
Jesuits also needed these texts to understand the local
customs and how the dates of traditional festivals were fixed by
Indians using the local calendar (“panchânga”). How the
mathematics given in these Indian ancient texts subsequently
diffused into 
 Marcus
du Sautoy
Marcus
du Sautoy Prof
K Ramasubramanian of IIT-Bombay has recently released
two-volume translation of the Ganita-Yukti-Bhasa
by Jyesthdeva points to the fact that
some subsets of calculus existed in Indian manuscripts almost two
centuries before Isaac Newton published his work.
Prof
K Ramasubramanian of IIT-Bombay has recently released
two-volume translation of the Ganita-Yukti-Bhasa
by Jyesthdeva points to the fact that
some subsets of calculus existed in Indian manuscripts almost two
centuries before Isaac Newton published his work.  Dr
George Gheverghese Joseph from the
Dr
George Gheverghese Joseph from the  Brian
Clegg ( ? ) author of popular science books has
written:
Brian
Clegg ( ? ) author of popular science books has
written:  David
Mumford, the eminent mathematician writes in his review of the book, Mathematics
in India by Kim
David
Mumford, the eminent mathematician writes in his review of the book, Mathematics
in India by Kim 




 Soviet historians, K.
Antonova, G. Bongard-Levin, and G. Kotovsky, authors of
Soviet historians, K.
Antonova, G. Bongard-Levin, and G. Kotovsky, authors of 
 Brahmagupta
(598 A.D. - 665 A.D.) is renowned for introduction of negative numbers and
operations on zero into arithmetic. His main work was Brahmasphutasiddhanta,
which was a corrected version of old astronomical treatise Brahmasiddhanta.
This work was later translated into Arabic as Sind
Hind. He formulated the rule of three and proposed
rules for the solution of quadratic and simultaneous equations. He was the first mathematician to treat algebra and
arithmetic as two different branches of mathematics. He gave the solution of the
indeterminate equation Nx2+1 = y2. He is also the founder
of the branch of higher mathematics known as "Numerical Analysis".
Brahmagupta
(598 A.D. - 665 A.D.) is renowned for introduction of negative numbers and
operations on zero into arithmetic. His main work was Brahmasphutasiddhanta,
which was a corrected version of old astronomical treatise Brahmasiddhanta.
This work was later translated into Arabic as Sind
Hind. He formulated the rule of three and proposed
rules for the solution of quadratic and simultaneous equations. He was the first mathematician to treat algebra and
arithmetic as two different branches of mathematics. He gave the solution of the
indeterminate equation Nx2+1 = y2. He is also the founder
of the branch of higher mathematics known as "Numerical Analysis".
 Vedic altars and sacrificial places were constructed
according to strict geometrical principles. The
Vedic (altar) had to be stacked in a geometrical form with the sides in fixed
proportions, and brick altars had to combine fixed dimensions with a fixed
number of bricks. Again, the surface areas were so designed that altars could be
increased in size without change of shape, which required considerable
geometrical ingenuity.
Vedic altars and sacrificial places were constructed
according to strict geometrical principles. The
Vedic (altar) had to be stacked in a geometrical form with the sides in fixed
proportions, and brick altars had to combine fixed dimensions with a fixed
number of bricks. Again, the surface areas were so designed that altars could be
increased in size without change of shape, which required considerable
geometrical ingenuity. Professor
H. G. Rawlinson writes: " It is more likely that Pythagoras was
influenced by India than by Egypt. Almost all the theories, religions,
philosophical and mathematical taught by the Pythagoreans, were known in India
in the sixth century B.C., and the Pythagoreans, like the Jains and the
Buddhists, refrained from the destruction of life and eating meat and regarded
certain vegetables such as beans as taboo" "It seems that the
so-called Pythagorean theorem of the quadrature of the hypotenuse was already
known to the Indians in the older Vedic times, and thus before Pythagoras
Professor
H. G. Rawlinson writes: " It is more likely that Pythagoras was
influenced by India than by Egypt. Almost all the theories, religions,
philosophical and mathematical taught by the Pythagoreans, were known in India
in the sixth century B.C., and the Pythagoreans, like the Jains and the
Buddhists, refrained from the destruction of life and eating meat and regarded
certain vegetables such as beans as taboo" "It seems that the
so-called Pythagorean theorem of the quadrature of the hypotenuse was already
known to the Indians in the older Vedic times, and thus before Pythagoras  Sir
William Temple, (1628-1699) English
statesman and diplomat, in his Essay upon the Ancient
and Modern Learning (1690) he wrote:
Sir
William Temple, (1628-1699) English
statesman and diplomat, in his Essay upon the Ancient
and Modern Learning (1690) he wrote: The
rules for measurement and construction of sacrificial altars are found in the
Sulba Sutras, the earliest documents of geometry in India. Sulba means cord. Of
the various Sulba Sutras, those of Baudhayana, Apastamba and Katyayana are best
known. The mathematical knowledge in the texts comes from the creation of altars
or bricks in various shapes-rhombus, isosceles trapezium, square, rectangle,
isosceles right-angled triangle or circle. A square-shaped altar sometimes had
to become circular without any change in the area or vice-versa. Obviously, the
authors of the Sulba texts knew the value of pi, which is the ratio of the
circumference to the diameter of a circle.
The
rules for measurement and construction of sacrificial altars are found in the
Sulba Sutras, the earliest documents of geometry in India. Sulba means cord. Of
the various Sulba Sutras, those of Baudhayana, Apastamba and Katyayana are best
known. The mathematical knowledge in the texts comes from the creation of altars
or bricks in various shapes-rhombus, isosceles trapezium, square, rectangle,
isosceles right-angled triangle or circle. A square-shaped altar sometimes had
to become circular without any change in the area or vice-versa. Obviously, the
authors of the Sulba texts knew the value of pi, which is the ratio of the
circumference to the diameter of a circle. In his monumental work, The origin of
mathematics, Archive for History of Exact Sciences.
vol. 18, 301-342, Abraham Seidenberg
remarks:
"By
examining the evidence in the Shatapatha
Brahmana, we now know that Indian
geometry predates Greek geometry by centuries. For example, the earth was
represented by a circular altar and the heavens were represented by a square
altar and the ritual consisted of converting the circle into a square of an
identical area. There we see the beginnings of geometry! Two aspects of the 'Pythagoras' theorem are described
in the Vedic literature. One aspect is purely algebraic that presents numbers
a, b, c for which the sum of the squares of the first two equals the square of
the third. The second is the geometric, according to which the sum of the
areas of two square areas of different size is equal to another square. The
Babylonians knew the algebraic aspect of this theorem as early as 1700 BCE,
but they did not seem to know the geometric aspect. The Shatapatha Brahmana,
which precedes the age of Pythagoras, knows both aspects. Therefore, the
Indians could not have learnt it from the Old-Babylonians or the Greeks, who
claim to have rediscovered the result only with Pythagoras. India is thus the
cradle of the knowledge of geometry and mathematics."
In his monumental work, The origin of
mathematics, Archive for History of Exact Sciences.
vol. 18, 301-342, Abraham Seidenberg
remarks:
"By
examining the evidence in the Shatapatha
Brahmana, we now know that Indian
geometry predates Greek geometry by centuries. For example, the earth was
represented by a circular altar and the heavens were represented by a square
altar and the ritual consisted of converting the circle into a square of an
identical area. There we see the beginnings of geometry! Two aspects of the 'Pythagoras' theorem are described
in the Vedic literature. One aspect is purely algebraic that presents numbers
a, b, c for which the sum of the squares of the first two equals the square of
the third. The second is the geometric, according to which the sum of the
areas of two square areas of different size is equal to another square. The
Babylonians knew the algebraic aspect of this theorem as early as 1700 BCE,
but they did not seem to know the geometric aspect. The Shatapatha Brahmana,
which precedes the age of Pythagoras, knows both aspects. Therefore, the
Indians could not have learnt it from the Old-Babylonians or the Greeks, who
claim to have rediscovered the result only with Pythagoras. India is thus the
cradle of the knowledge of geometry and mathematics." 
 Ramanujan is one of
India´s great intellectual heroes, a
mathematical genius who attributed his brilliance to a personal
relationship with a Hindu Goddess -
Namagiri. His work has been used to help
unravel knots as varied as polymer chemistry and cancer, yet how
he arrived at this theorems is still unknown. By age twelve he had mastered trigonometry so completely
that he was inventing sophisticated theorems that astonished
teachers. Mathematicians have mined his
theorems ever since. They've figured out how to prove them.
They've put them to use. Only recently, a lost bundle of his
notebooks turned up in a Cambridge library. That set mathematics
off on a whole new voyage of discovery. And
where did all this unproven truth come from? Ramanujan was quick
to tell us. He simply prayed to Sarasvathi,
the Goddess of Learning, and she informed him.
Ramanujan is one of
India´s great intellectual heroes, a
mathematical genius who attributed his brilliance to a personal
relationship with a Hindu Goddess -
Namagiri. His work has been used to help
unravel knots as varied as polymer chemistry and cancer, yet how
he arrived at this theorems is still unknown. By age twelve he had mastered trigonometry so completely
that he was inventing sophisticated theorems that astonished
teachers. Mathematicians have mined his
theorems ever since. They've figured out how to prove them.
They've put them to use. Only recently, a lost bundle of his
notebooks turned up in a Cambridge library. That set mathematics
off on a whole new voyage of discovery. And
where did all this unproven truth come from? Ramanujan was quick
to tell us. He simply prayed to Sarasvathi,
the Goddess of Learning, and she informed him.
 Born
in the Vedic Age, but buried under centuries of debris, this
remarkable system of calculation was deciphered towards the
beginning of the 20th century, when there was a great interest in
ancient Sanskrit texts, especially in Europe. However, certain
texts called Ganita Sutras,
which contained mathematical deductions, were ignored, because no
one could find any mathematics in them. These texts, it's
believed, bore the germs of what we now know as Vedic Mathematics.
Born
in the Vedic Age, but buried under centuries of debris, this
remarkable system of calculation was deciphered towards the
beginning of the 20th century, when there was a great interest in
ancient Sanskrit texts, especially in Europe. However, certain
texts called Ganita Sutras,
which contained mathematical deductions, were ignored, because no
one could find any mathematics in them. These texts, it's
believed, bore the germs of what we now know as Vedic Mathematics. According to
According to

 Leonard
Bloomfield (1887-1949) American
linguist and author of
Leonard
Bloomfield (1887-1949) American
linguist and author of  Panini and other
grammarians, especially Katyayana and Patanjali, carried the work much further,
and by the middle of the second century B.C. Sanskrit had attained a stereotyped
form which remained unaltered for centuries. Whilst Greek grammar tended to be
logical, philosophical and syntactical, Indian grammar was the result of an
empirical investigation of language done with the objectivity of an anatomist
dissecting a body.
Panini and other
grammarians, especially Katyayana and Patanjali, carried the work much further,
and by the middle of the second century B.C. Sanskrit had attained a stereotyped
form which remained unaltered for centuries. Whilst Greek grammar tended to be
logical, philosophical and syntactical, Indian grammar was the result of an
empirical investigation of language done with the objectivity of an anatomist
dissecting a body. 

 The campus
accommodated 10,500 students and
offered over sixty different courses in various fields, such as
science, mathematics, medicine, politics, warfare, astrology,
astronomy, music, religion, and philosophy. The minimum age for
admission was 16 years and students from as far as Babylonia,
Greece, Syria, Arabia, and China came to study at the
university. Taxila,
stood on the banks of the river Vitasa in the northwest of the
Indian subcontinent.
The campus
accommodated 10,500 students and
offered over sixty different courses in various fields, such as
science, mathematics, medicine, politics, warfare, astrology,
astronomy, music, religion, and philosophy. The minimum age for
admission was 16 years and students from as far as Babylonia,
Greece, Syria, Arabia, and China came to study at the
university. Taxila,
stood on the banks of the river Vitasa in the northwest of the
Indian subcontinent.  It
had ten thousand students, one hundred lecture-rroms, great
libraries, and six immense blocks of dormitories four stories high;
its observatories, said Yuan
Chwang,
"were lost in the vapors of the morning, and the upper rooms
towered above the clouds." The old Chinese pilgrim loved the
learned monks and shady groves of Nalanda so well he stayed there
for five years.
It
had ten thousand students, one hundred lecture-rroms, great
libraries, and six immense blocks of dormitories four stories high;
its observatories, said Yuan
Chwang,
"were lost in the vapors of the morning, and the upper rooms
towered above the clouds." The old Chinese pilgrim loved the
learned monks and shady groves of Nalanda so well he stayed there
for five years.  (source:
(source: 
 Coinage
dating from the 8th Century B.C. to the17th Century A.D. Numismatic evidence of
the advances made by Smelting technology in ancient India. The image of Nataraja
the God of Dance is made of
five metals (Pancha-Dhatu). This technology of mixing two or more metals
and deriving superior alloys has been observed and noted by the Greek Historian Philostratus.
The
Makara (Spire) over Hindu temples were always adorned with brass or gold
toppings (Kamandals). The earliest reference to the advances made in Smelting
technology in India are by Greek historians viz, Philostratus and Ktesias in the
4th century B.C.
Coinage
dating from the 8th Century B.C. to the17th Century A.D. Numismatic evidence of
the advances made by Smelting technology in ancient India. The image of Nataraja
the God of Dance is made of
five metals (Pancha-Dhatu). This technology of mixing two or more metals
and deriving superior alloys has been observed and noted by the Greek Historian Philostratus.
The
Makara (Spire) over Hindu temples were always adorned with brass or gold
toppings (Kamandals). The earliest reference to the advances made in Smelting
technology in India are by Greek historians viz, Philostratus and Ktesias in the
4th century B.C.
 Nanotechnology
Nanotechnology Traditional
Indian iron and steel are known to have some very special properties such as
resistance to corrosion. This is substantiated by the 1600-year-old, twenty-five
feet high iron pillar next to the Qutub Minar in New Delhi, believed to have
been installed during Chandragupta Maurya's reign.
The famous iron pillar in Delhi belonging to the
fourth-fifth century A.D. is a metallurgical wonder. This huge wrought iron
pillar, 24 feet in height 16.4 inches in diameter at the bottom, and 6 1/2 tons
in weight has stood exposed to tropical sun and rain for fifteen hundred years,
but does not show the least sign of rusting or corrosion. Evidence shows
that the pillar was once a Garuda Stambha
from a Vishnu temple.
This pillar was plundered by Islamic hoards from a temple dedicated to Vishnu
and added as a trophy in the Quwwat al-Islam mosque in Delhi. Made of pure iron, which even today can be produced only
in small quantities by electrolysis. Such a pillar would be most difficult to
make even today. Thus, the pillar defies explanation.
Traditional
Indian iron and steel are known to have some very special properties such as
resistance to corrosion. This is substantiated by the 1600-year-old, twenty-five
feet high iron pillar next to the Qutub Minar in New Delhi, believed to have
been installed during Chandragupta Maurya's reign.
The famous iron pillar in Delhi belonging to the
fourth-fifth century A.D. is a metallurgical wonder. This huge wrought iron
pillar, 24 feet in height 16.4 inches in diameter at the bottom, and 6 1/2 tons
in weight has stood exposed to tropical sun and rain for fifteen hundred years,
but does not show the least sign of rusting or corrosion. Evidence shows
that the pillar was once a Garuda Stambha
from a Vishnu temple.
This pillar was plundered by Islamic hoards from a temple dedicated to Vishnu
and added as a trophy in the Quwwat al-Islam mosque in Delhi. Made of pure iron, which even today can be produced only
in small quantities by electrolysis. Such a pillar would be most difficult to
make even today. Thus, the pillar defies explanation. The
Delhi Iron Pillar is a testimony to the high level of skill
achieved by the ancient Indian ironsmiths in the extraction and
processing of iron.
The
Delhi Iron Pillar is a testimony to the high level of skill
achieved by the ancient Indian ironsmiths in the extraction and
processing of iron.  In 1961, the pillar (23 feet and 8
inches, and 6 tonnes) was dug out for chemical treatment and
preservation and reinstalled by embedding the underground part in a
masonry pedestal. Chemical analyses have indicated that the pillar
was astonishingly pure or low in carbon compared with modern
commercial iron.
In 1961, the pillar (23 feet and 8
inches, and 6 tonnes) was dug out for chemical treatment and
preservation and reinstalled by embedding the underground part in a
masonry pedestal. Chemical analyses have indicated that the pillar
was astonishingly pure or low in carbon compared with modern
commercial iron. It was only
some three decades later that this view was revised. An earlier
revision in fact, even when confronted with contrary evidence as
was made available by other observers of the Indian techniques
and processes, was intellectual impossibility. "That iron
could be converted into cast steel by fusing it in a close
vessel in contact with carbon" was yet to be discovered,
and it was only in 1825 that a British manufacturer "took
out a patent for converting iron into steel by exposing it to
the action of caruretted hydrogen gas in a close vessel, at a
very high temperature, by which means the process of conversion
is completed in a few hours, while by the old method, it was the
work of from 14 to 20 days."
It was only
some three decades later that this view was revised. An earlier
revision in fact, even when confronted with contrary evidence as
was made available by other observers of the Indian techniques
and processes, was intellectual impossibility. "That iron
could be converted into cast steel by fusing it in a close
vessel in contact with carbon" was yet to be discovered,
and it was only in 1825 that a British manufacturer "took
out a patent for converting iron into steel by exposing it to
the action of caruretted hydrogen gas in a close vessel, at a
very high temperature, by which means the process of conversion
is completed in a few hours, while by the old method, it was the
work of from 14 to 20 days."  Writings:
The earliest known reference to diamond is a Sanskrit manuscript,
the Arthasastra ("The
Lesson of Profit") by Kautiliya,
a minister to Chandragupta of the Mauryan dynasty in northern
India. The work is dated from 320-296 before the Common Era (BCE).
Kautiliya states "(a diamond that is) big, heavy, capable of
bearing blows, with symmetrical points, capable of scratching
(from the inside) a (glass) vessel (filled with water), revolving
like a spindle and brilliantly shining is excellent. That
(diamond) with points lost, without edges and defective on one
side is bad." Indians recognized the qualities of a fine
diamond octahedron and valued it.
Writings:
The earliest known reference to diamond is a Sanskrit manuscript,
the Arthasastra ("The
Lesson of Profit") by Kautiliya,
a minister to Chandragupta of the Mauryan dynasty in northern
India. The work is dated from 320-296 before the Common Era (BCE).
Kautiliya states "(a diamond that is) big, heavy, capable of
bearing blows, with symmetrical points, capable of scratching
(from the inside) a (glass) vessel (filled with water), revolving
like a spindle and brilliantly shining is excellent. That
(diamond) with points lost, without edges and defective on one
side is bad." Indians recognized the qualities of a fine
diamond octahedron and valued it. In regard to military science, the Ramayana and the
Puranas make frequent mention of Shataghnis,
or canons, being placed on forts and used in times of emergency. A canon was
called
"Shataghni"
because it meant the fire weapon that kills one
hundred men at once. They ascribe these
agniyastras, or weapons of fire, to
Visvakarma, the architect of the Vedic epics. Rockets were also Indian
inventions and were used in native armies when Europeans first came into contact
with them. As per Dante's Inferno,
Alexander mentioned in a letter to Aristotle, that terrific flashes of flame
showered on his army in India. The Shukra Neeti is
an ancient text that deals with the manufacture of arms such as rifles and guns.
In The Celtic Druids (pp-115-116),
Godfrey Higgins provides
evidence that Hindus knew of gun powder from the remotest antiquity.
In regard to military science, the Ramayana and the
Puranas make frequent mention of Shataghnis,
or canons, being placed on forts and used in times of emergency. A canon was
called
"Shataghni"
because it meant the fire weapon that kills one
hundred men at once. They ascribe these
agniyastras, or weapons of fire, to
Visvakarma, the architect of the Vedic epics. Rockets were also Indian
inventions and were used in native armies when Europeans first came into contact
with them. As per Dante's Inferno,
Alexander mentioned in a letter to Aristotle, that terrific flashes of flame
showered on his army in India. The Shukra Neeti is
an ancient text that deals with the manufacture of arms such as rifles and guns.
In The Celtic Druids (pp-115-116),
Godfrey Higgins provides
evidence that Hindus knew of gun powder from the remotest antiquity.
 “The
ancient Hindus could navigate the air, and not only navigate it, but
fight battles in it like so many war-eagles combating for the
domination of the clouds. To be so perfect in aeronautics, they must
have known all the arts and sciences related to the science,
including the strata and currents of the atmosphere, the relative
temperature, humidity, density and specific gravity of the various
gases...”
“The
ancient Hindus could navigate the air, and not only navigate it, but
fight battles in it like so many war-eagles combating for the
domination of the clouds. To be so perfect in aeronautics, they must
have known all the arts and sciences related to the science,
including the strata and currents of the atmosphere, the relative
temperature, humidity, density and specific gravity of the various
gases...” 
 The art
of Navigation was born in the river Sindh 6000 years ago. The very word Navigation is
derived from the Sanskrit word
NAV Gatih.
The art
of Navigation was born in the river Sindh 6000 years ago. The very word Navigation is
derived from the Sanskrit word
NAV Gatih.

 Sardar
Kavalam Madhava Panikkar
Sardar
Kavalam Madhava Panikkar Professor Georg Buehler (1837-1898)
the German Orientalist, had said:
Professor Georg Buehler (1837-1898)
the German Orientalist, had said:
 The influence of the sea on Indian kingdoms
continued to grow with the passage of time. North-west India came under the
influence of Alexander, who built a harbor at Patala where the Indus branches
into two just before entering the Arabian Sea. His army returned to Mesopotamia
in ships built in Sind. Records show that in the period after his conquest,
Chandragupta
Maurya established an Admiralty Division under a Superintendent of Ships as part
of his war office, with a charter including responsibility for navigation on the
seas, oceans, lakes and rivers.
History
records that Indian ships traded with countries as far as Java and Sumatra, and
available evidence indicates that they were also trading with other countries in
the Pacific and Indian Oceans. Even before Alexander there were references to
India in Greek works, and India had a flourishing trade with Rome.
The
Roman writer Pliny
speaks of Indian traders carrying away large quantities of
gold from Rome, in payment for much-sought exports such as precious stones,
skins, clothes, spices, sandalwood, perfumes, herbs and indigo.
The influence of the sea on Indian kingdoms
continued to grow with the passage of time. North-west India came under the
influence of Alexander, who built a harbor at Patala where the Indus branches
into two just before entering the Arabian Sea. His army returned to Mesopotamia
in ships built in Sind. Records show that in the period after his conquest,
Chandragupta
Maurya established an Admiralty Division under a Superintendent of Ships as part
of his war office, with a charter including responsibility for navigation on the
seas, oceans, lakes and rivers.
History
records that Indian ships traded with countries as far as Java and Sumatra, and
available evidence indicates that they were also trading with other countries in
the Pacific and Indian Oceans. Even before Alexander there were references to
India in Greek works, and India had a flourishing trade with Rome.
The
Roman writer Pliny
speaks of Indian traders carrying away large quantities of
gold from Rome, in payment for much-sought exports such as precious stones,
skins, clothes, spices, sandalwood, perfumes, herbs and indigo. Between the fifth and tenth centuries AD, the
Vijaynagaram and Kalinga kingdoms of southern and eastern India had established
their rule over Malaya, Sumatra and Western Java. The Andaman and Nicobar
Islands then served as an important midway point for trade between the Indian
peninsula and these kingdoms, as also with China. The daily revenue from the
eastern regions in the period 844-848 AD was estimated at 200 maunds (eight
tons) of gold. In the period 984-1042 AD, the Chola kings dispatched great naval
expeditions which occupied parts of Burma, Malaya and Sumatra, while suppressing
the piratical activities of the Sumatran warlords. In
1292 AD,
Marco Polo described Indian ships as " ...built of fir timber,
having a sheath of boards laid over the planking in every part, caulked with
oakum and fastened with iron nails. The bottoms were smeared with a preparation
of quicklime and hemp, pounded together and mixed with oil from a certain tree
which is a better material than pitch."
Between the fifth and tenth centuries AD, the
Vijaynagaram and Kalinga kingdoms of southern and eastern India had established
their rule over Malaya, Sumatra and Western Java. The Andaman and Nicobar
Islands then served as an important midway point for trade between the Indian
peninsula and these kingdoms, as also with China. The daily revenue from the
eastern regions in the period 844-848 AD was estimated at 200 maunds (eight
tons) of gold. In the period 984-1042 AD, the Chola kings dispatched great naval
expeditions which occupied parts of Burma, Malaya and Sumatra, while suppressing
the piratical activities of the Sumatran warlords. In
1292 AD,
Marco Polo described Indian ships as " ...built of fir timber,
having a sheath of boards laid over the planking in every part, caulked with
oakum and fastened with iron nails. The bottoms were smeared with a preparation
of quicklime and hemp, pounded together and mixed with oil from a certain tree
which is a better material than pitch."
 A panel found at
Mohenjodaro, depicting a
sailing craft. Vessels were of many types. Their construction is vividly
described in the Yukti Kalpa Taru an ancient Indian text on Ship-building. There is evidence that a compass made by iron
fish floating in a vessel of oil and pointing north was used by mariners. The
typical Harappan seals have been found far a field in Oman, Mesopotamia, and the
Maldives. These finds bear witness to the enthusiastic initiative of the early
Indic peoples as sea faring merchants.
A panel found at
Mohenjodaro, depicting a
sailing craft. Vessels were of many types. Their construction is vividly
described in the Yukti Kalpa Taru an ancient Indian text on Ship-building. There is evidence that a compass made by iron
fish floating in a vessel of oil and pointing north was used by mariners. The
typical Harappan seals have been found far a field in Oman, Mesopotamia, and the
Maldives. These finds bear witness to the enthusiastic initiative of the early
Indic peoples as sea faring merchants. The art of shipbuilding and navigation in India and China at the time was
sufficiently advanced for oceanic crossings. Indian ships operating between Indian and
South-east Asian ports were large and well equipped to sail cross the Bay of Bengal. When
the Chinese Buddhist scholar, Fa-hsien, returned from India, his ship carried a crew of more than two hundred
persons and did not sail along the coasts but directly across the ocean. Such ships
were larger than those Columbus used to negotiate the Atlantic a thousand years later.
The art of shipbuilding and navigation in India and China at the time was
sufficiently advanced for oceanic crossings. Indian ships operating between Indian and
South-east Asian ports were large and well equipped to sail cross the Bay of Bengal. When
the Chinese Buddhist scholar, Fa-hsien, returned from India, his ship carried a crew of more than two hundred
persons and did not sail along the coasts but directly across the ocean. Such ships
were larger than those Columbus used to negotiate the Atlantic a thousand years later.  Sir
John Malcolm (1769 - 1833) was a Scottish soldier, statesman, and
historian entered the service of the East India Company wrote about Indian
vessels that they:
Sir
John Malcolm (1769 - 1833) was a Scottish soldier, statesman, and
historian entered the service of the East India Company wrote about Indian
vessels that they:

 Mrs.
Charlotte S Manning
Mrs.
Charlotte S Manning It
would be interesting to many to learn that “it was in India that
the Greeks first became acquainted with sugar.” Sugar bears a
name derived from Sanskrit. With the article the name traveled
into Arabia and Persia, and thence became established in the
languages of Europe.
It
would be interesting to many to learn that “it was in India that
the Greeks first became acquainted with sugar.” Sugar bears a
name derived from Sanskrit. With the article the name traveled
into Arabia and Persia, and thence became established in the
languages of Europe.  Arnold
Hermann Ludwig
Arnold
Hermann Ludwig

 An
idea of the immense wealth of India could be gathered from the
fact that when Sultan Mahmud Ghaznavi destroyed the far
famed temple of Somnath he found such immense riches
and astonishing diamonds cooped up in the single “Idol
of Shiva” that it was found quite impossible to calculate the
value of that booty.
An
idea of the immense wealth of India could be gathered from the
fact that when Sultan Mahmud Ghaznavi destroyed the far
famed temple of Somnath he found such immense riches
and astonishing diamonds cooped up in the single “Idol
of Shiva” that it was found quite impossible to calculate the
value of that booty.
 According
to Economist Angus Maddison
(1926 - ) in The World Economy: A
Millennial Perspective, the region that today comprises
the Indian subcontinent held the largest
share of the world's gross domestic product until the beginning of
the 16th century, when it was rivaled by China, and
then again throughout most of the 18th century.
According
to Economist Angus Maddison
(1926 - ) in The World Economy: A
Millennial Perspective, the region that today comprises
the Indian subcontinent held the largest
share of the world's gross domestic product until the beginning of
the 16th century, when it was rivaled by China, and
then again throughout most of the 18th century.  From
the early 18th century until the beginnings of the 19th century,
when India enjoyed a 24.4 % share of the world's gross domestic
product (see table) economic historian Paul Bairoch conforms, the
region enjoyed a 25 % share of the global trade in textiles. It
was the world's leading manufacturer of handicrafts and handloom
textiles.
From
the early 18th century until the beginnings of the 19th century,
when India enjoyed a 24.4 % share of the world's gross domestic
product (see table) economic historian Paul Bairoch conforms, the
region enjoyed a 25 % share of the global trade in textiles. It
was the world's leading manufacturer of handicrafts and handloom
textiles. 